(c) Philip Gibbs
LightMill animation by Torsten Hiddessen

Line driven winds

are accelerated by photon momentum The heating is minimal

Which objects?

Photospheres 10-50 kK strong UV field

O stars accretion disks: stars to quasars

Why study winds from massive stars?

influence on stellar evolution winds trigger star formation

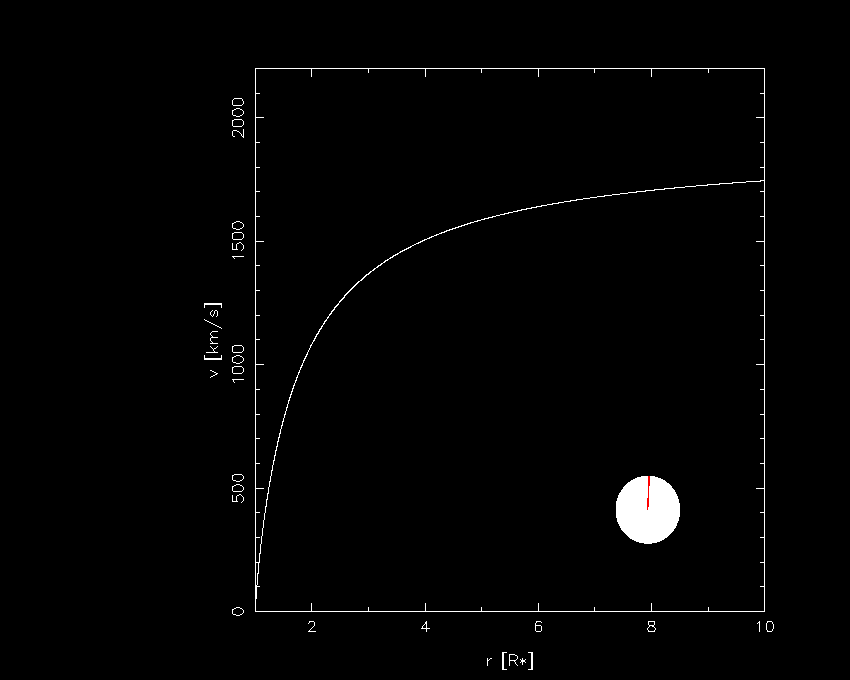
Stellar Wind

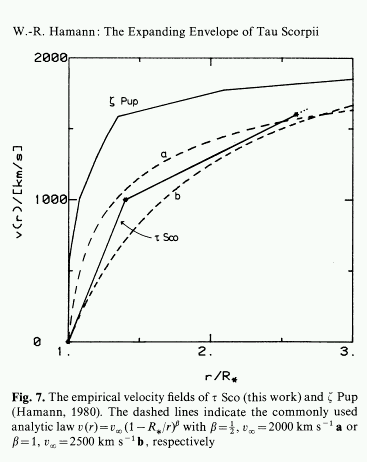
Recent interests in line driven hydrodynamics

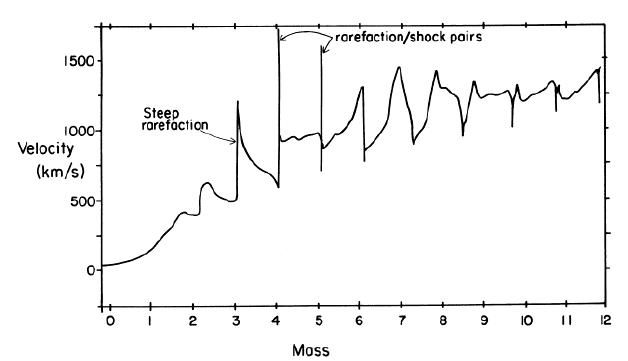	Shocks from line driven instability Owocki et al. 1988 ApJ
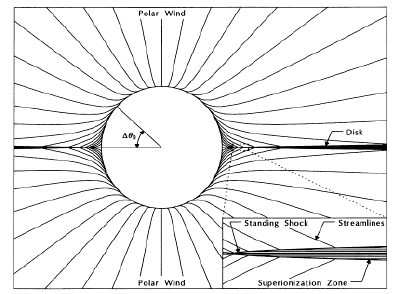	Wind compressed disks Bjorkman & Cassinelli 1993 ApJ
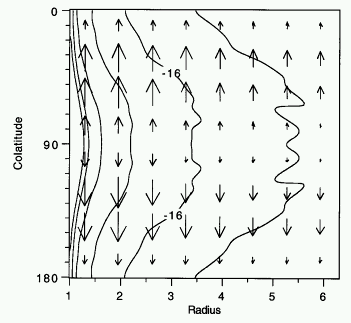	Disk inhibition Owocki et al. 1996 ApJ
	Corotating interaction regions Cranmer & Owocki 1996 ApJ
	High-mass X-ray binaries Blondin et al. 1990 ApJ
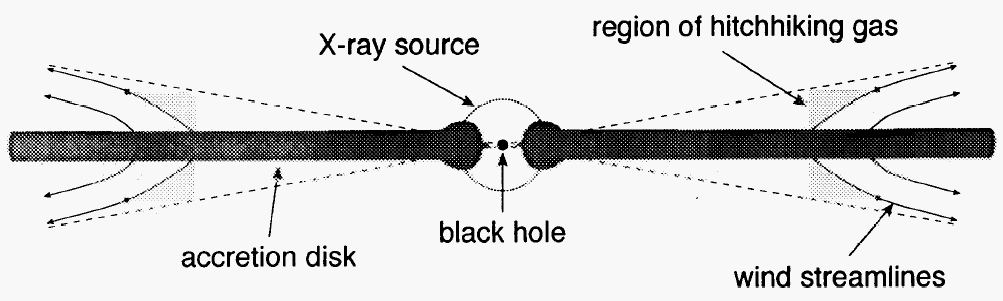
	Quasar winds Murray et al. 1995 ApJ
	Disk winds Feldmeier & Drew 2000 MNRAS

THE LINE FORCE

Two forces (out of 4)

Sobolev force 50 mesh points	SOB	Castor et al 1975	gl = Cr-2    æ è r-1 du/dr ö ø a   ,             0 < a < 1
Smooth source function force 5000 × 50 mesh points	SSF	Hamann 1980 Lamers 1986 Owocki 1991	gl = Cr-2 ó õ ¥ -¥  dy   f æ è y-u(r) ö ø æ ç è 1-S(r) t+a(y,r) + S(r) t-a(y,r) ö ÷ ø t+(y,r) = ó õ r   dr¢  r(r¢)  f æ è y-u(r¢) ö ø t-(y,r) = t max(r)  -  t+(y,r)
			f : Doppler line profile u: wind velocity / thermal speed y: normalized frequency r: wind density C: a constant

SOB causes new wave type

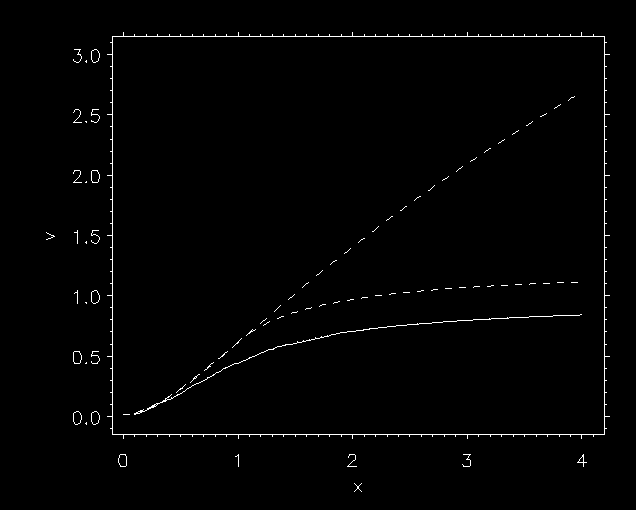
Abbott waves (1980):

a radiative wave mode

SSF: Abbott waves and 1A. DE-SHADOWING INSTABILITY

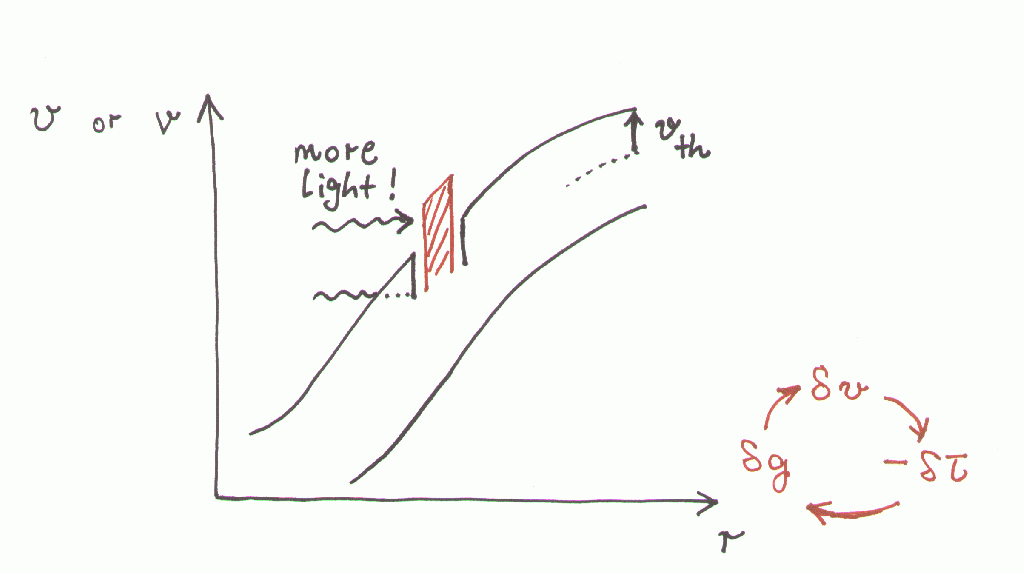
long scale limit: Abbott waves (1980 ApJ)

short scale limit: instability (Carlberg 1980 ApJ)

Bridging law from exact (!) ABS Owocki & Rybicki (1984 ApJ) Unstable waves from 2nd order SOB Feldmeier (1998 A&A)

Wind structure from numerical hydrodynamics

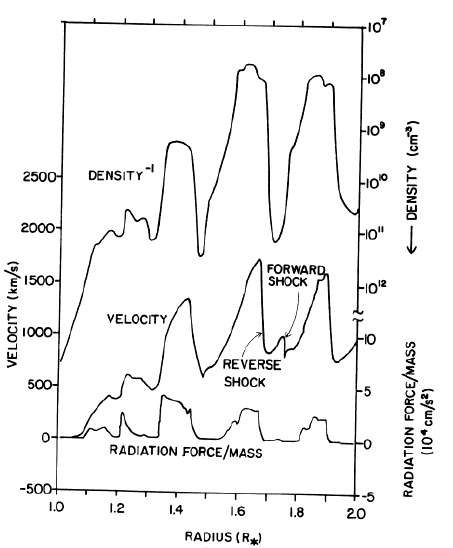
Owocki, Castor & Rybicki, 1988 ApJ

SSF
with S=0








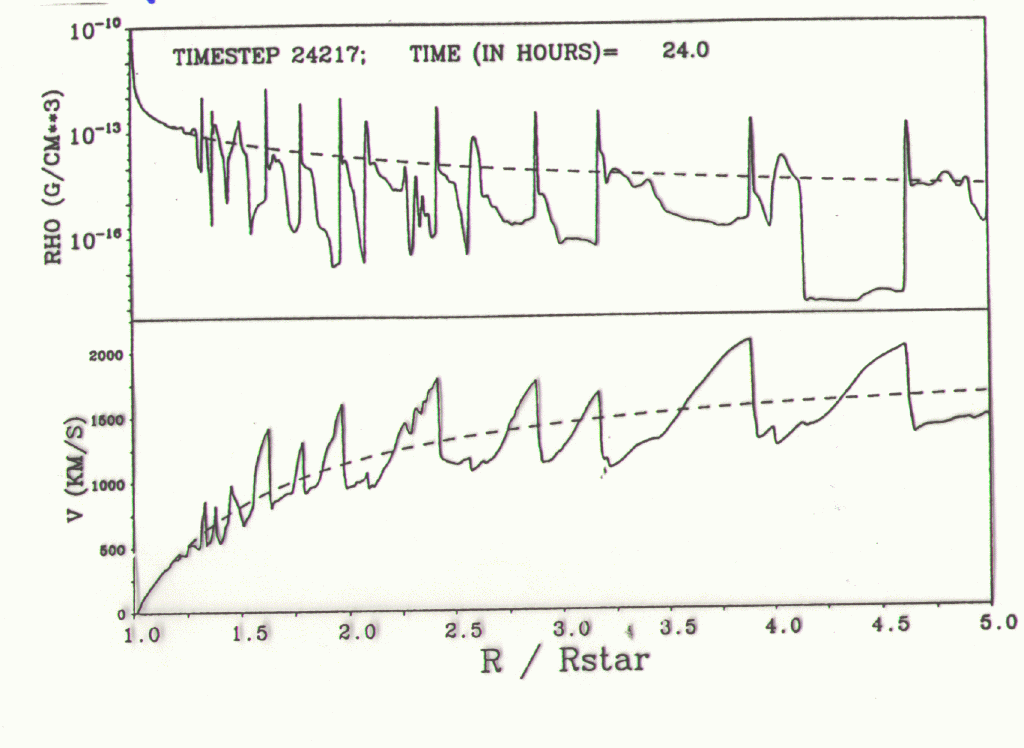
Feldmeier, 1995 A&A

SSF

Broad rarefactions regions of thin gas accelerated to large speeds

Very dense shells stop fast gas through reverse shock

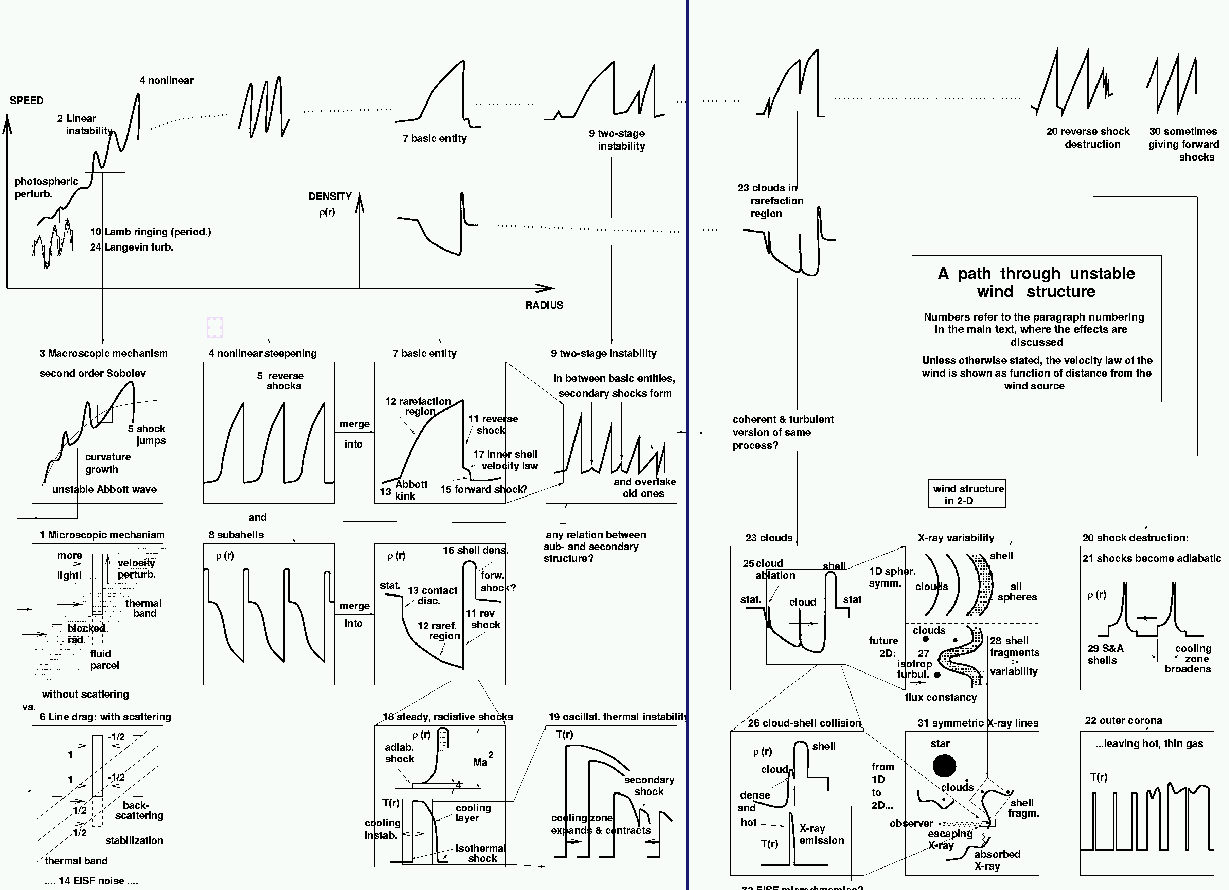
1B. X-RAYS AND CLOUDS

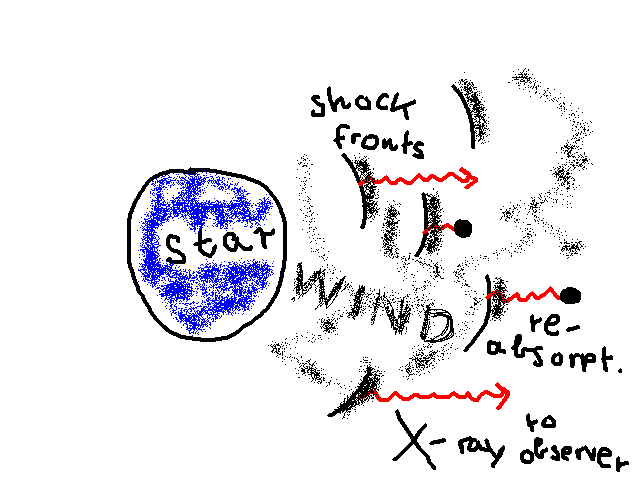
wind shocks as

X-ray sources in the wind

Lucy & White 1980 ApJ
Lucy 1982 ApJ

First problem

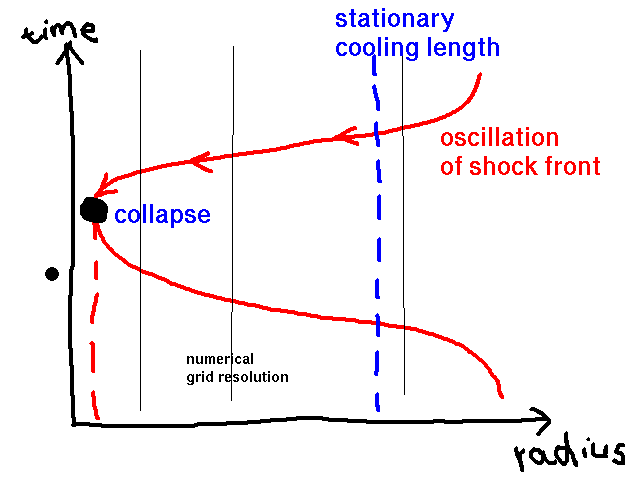
Thermal instability (Langer 1981 ApJ): cooling zone collapse Change cooling function at low T (F. 1994 Diss)

Second problem

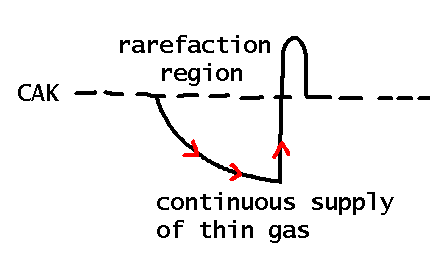
	density too small. Not enough X-rays (Hillier et al. 1994 A&A)
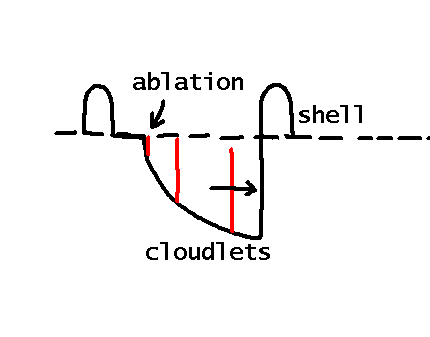
	solution: we propose (SSF) fast & dense cloudlets collide with shells (Feldmeier et al. 1997 A&A)

Wind model for zeta Ori, including energy transfer

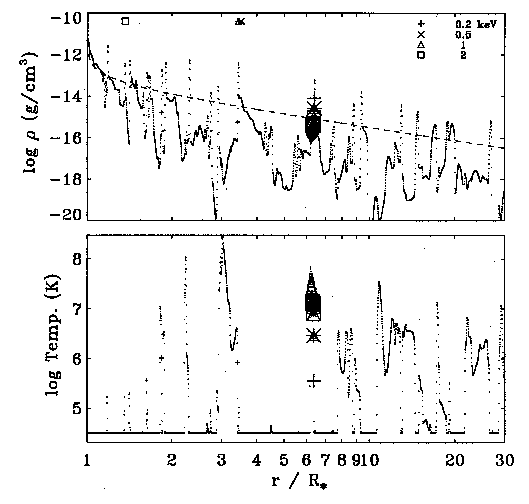	single wind location emitting X-rays
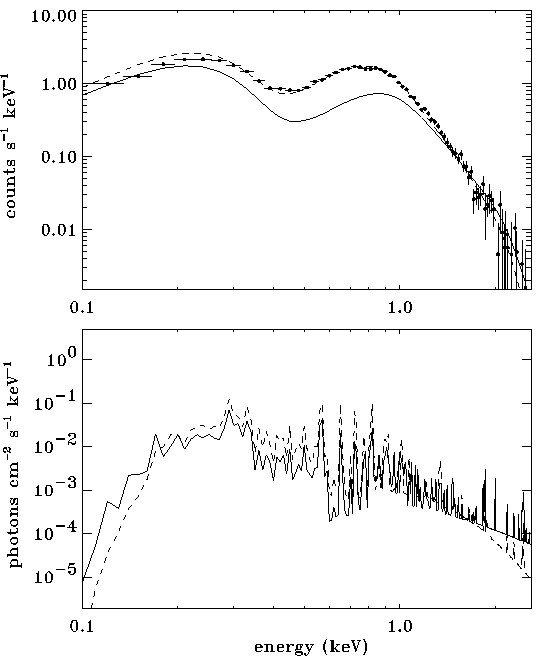	X-ray spectrum, compared to ROSAT data

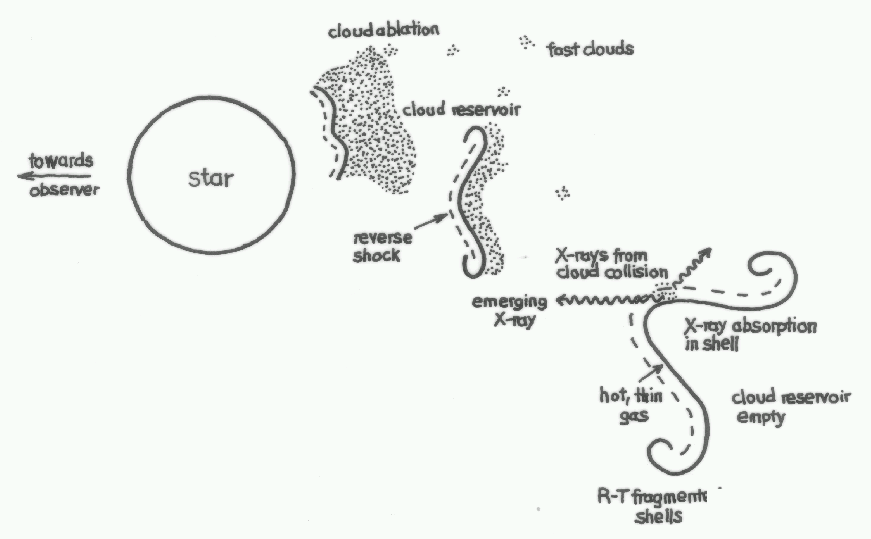
Cloud-shell collisions

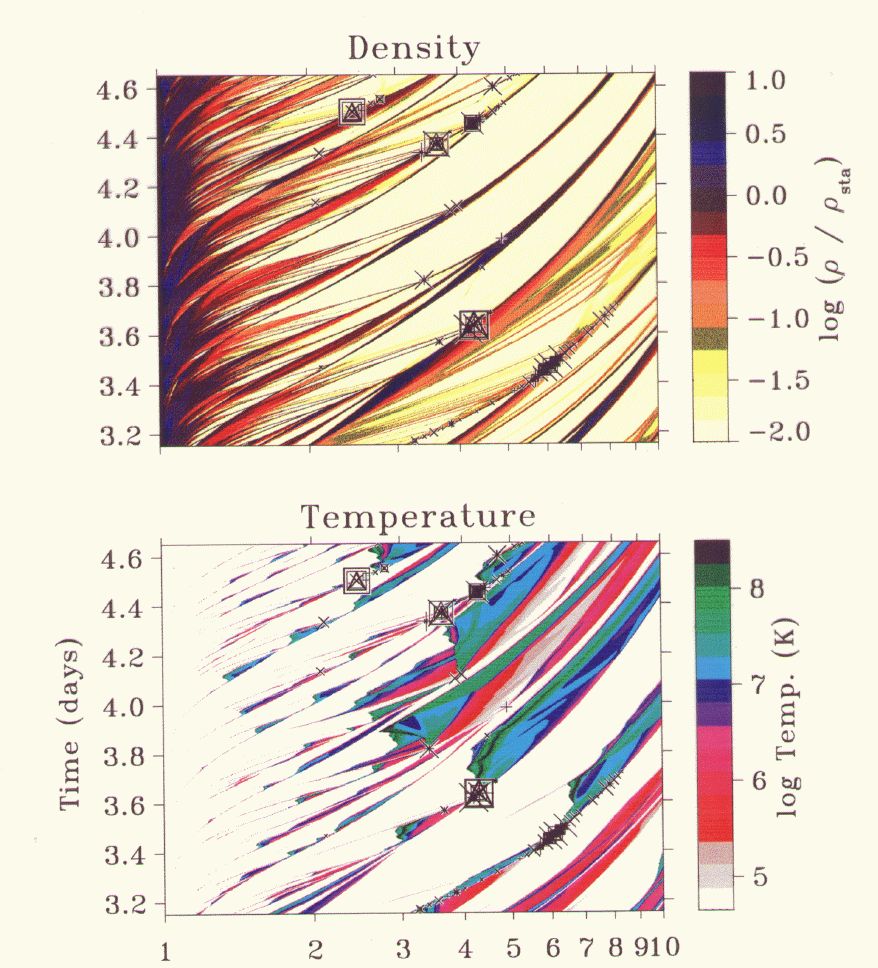
SSF

• numerous clouds
• all X-rays from cloud-shell collisions
• average X-ray emission agrees with ROSAT data

Cassinelli et al. 2001 ApJ: ``... zeta Pup and other OB stars. Wind-shock models developed by Lucy & White (1980), Feldmeier et al. (1997a) and others consistently failed to predict the high levels of X-ray emission observed in the brightest O stars.''

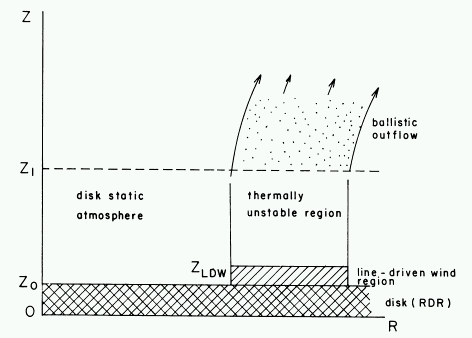
2. DISK WINDS

current computers: SOB


Winds from accretion disks in

• Protostars (YSOs)
• Cataclysmic variables
• Quasars

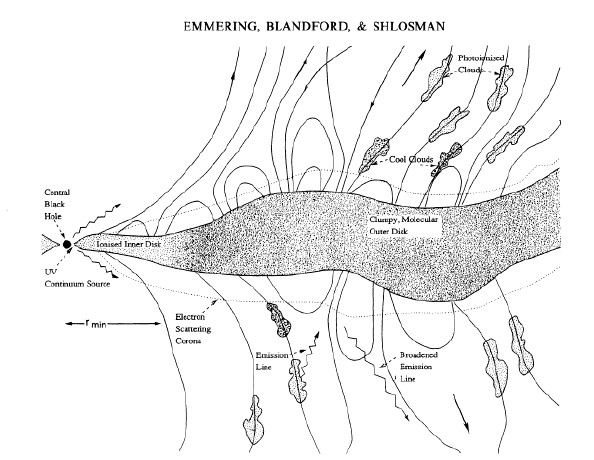
Shlosman et al. 1985. Disk radiation launches quasar wind. Central engine shielded by absorption in disk atmosphere.

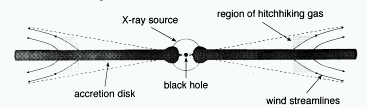
Murray et al. 1995. Central engine shielded by hitchhiking gas.

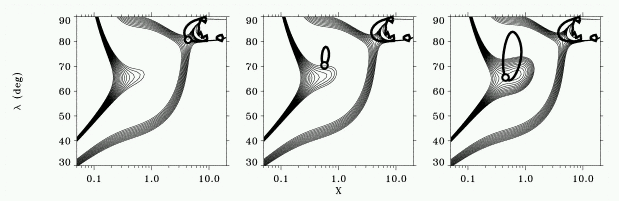
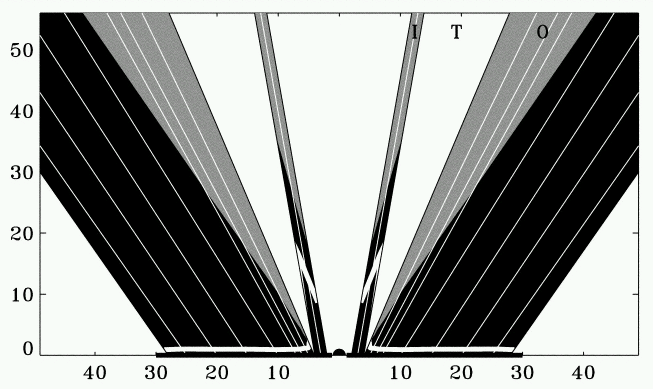
DISK WIND MOVIE

Results agree well with semi-analytical model
(Feldmeier & Shlosman 1999a,b ApJ)

Traditionally: disk winds magnetically driven (YSOs; quasars?)

Here: radiation driven (CVs; quasars?)

try now: combination

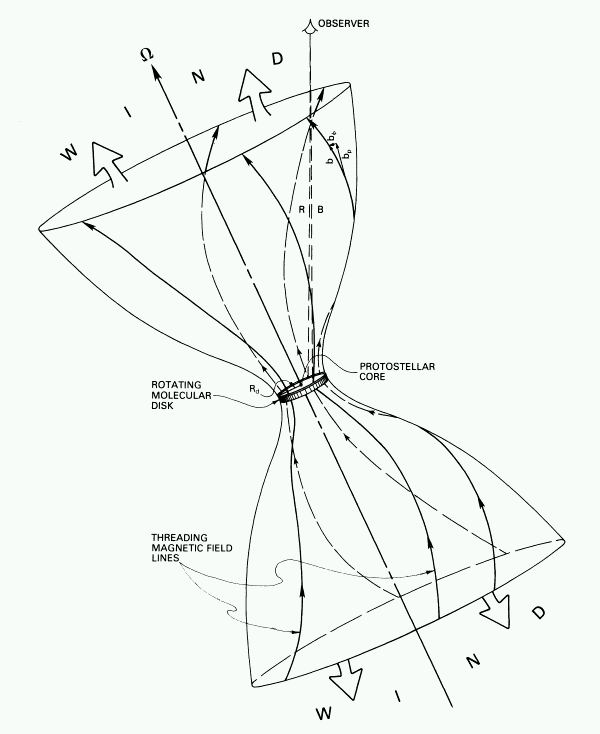
Hour-glass model of
poloidal field amplification

Norman and Pudritz 1986 ApJ




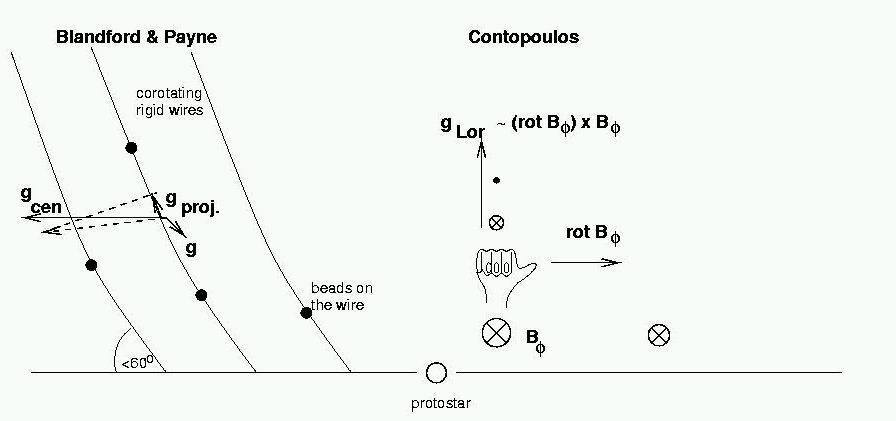
after Blandford & Payne 1982 MNRAS

We find that Zeus-MHD+SOB favors another scenario first suggested by Contopoulos 1995 ApJ

Here, strong toroidal magnetic fields occur.

Wind is launched via Lorentz force along vertical gradients of toroidal field. By contrast, B&P82 launichg via centrifugal force along poloidal field.

Vortex sheet in poloidal magnetic field unit arrow (top right) = 0.5 Gauss

A poloidal-toroidal interaction

Vortex sheet in poloidal field Poloidal eddies carry toroidal field to large height Lorentz force (toroidal field) drives enhanced mass loss

3. ABBOTT WAVES AND RUNAWAY

Time-averaged SSF solutions, or
Steady, stable SOB solutions

Question

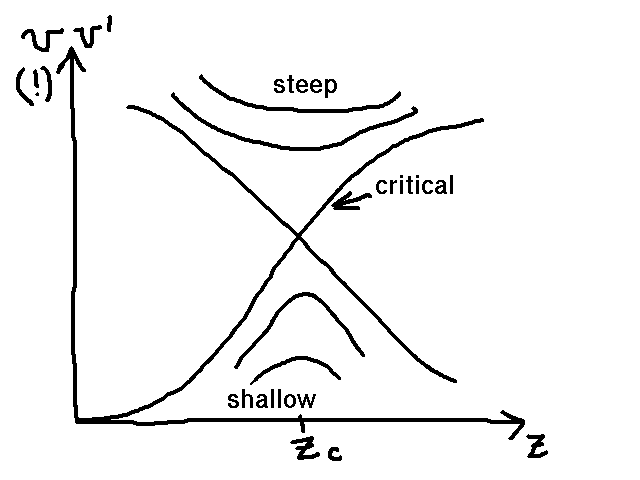
Why does the wind adopt the critical solution
out of an infinite solution variety?





Castor et al. 1975 ApJ,
Abbott 1980 ApJ:
shallow solutions do not reach infinity
Steep solutions do not reach photosphere
-> mixed sS or critical




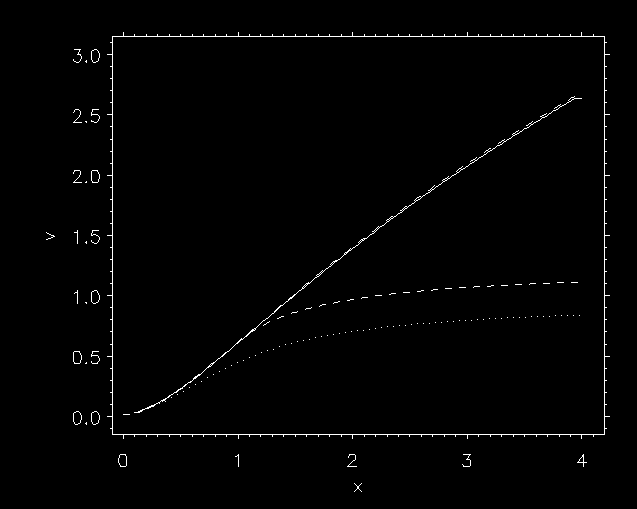Artificial convergence to sS CAK solution:

1. outflow boundary conditions
2. NO Abbott time step

(Feldmeier, Shlosman & Hamann 2002 ApJ)

SOB

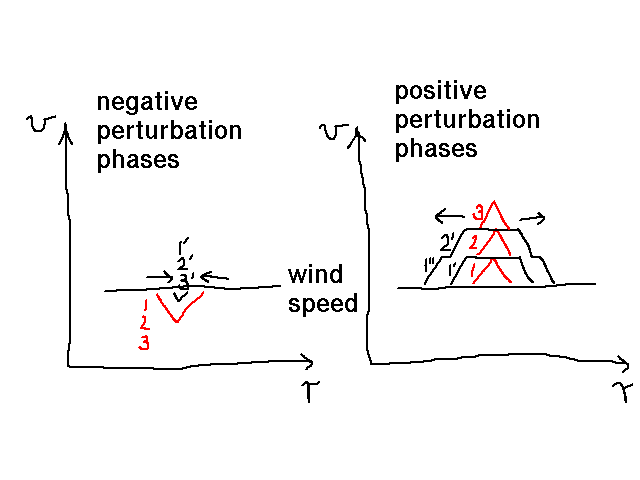
Abbott wave runaway

Strange Abbott wave dispersion: Positive v-slopes propagate inwards Negative v-slopes propagate outwards -> systematic wind acceleration: runaway (Feldmeier & Shlosman 2000, 2002 ApJ)

SOB



Runaway of shallow solution











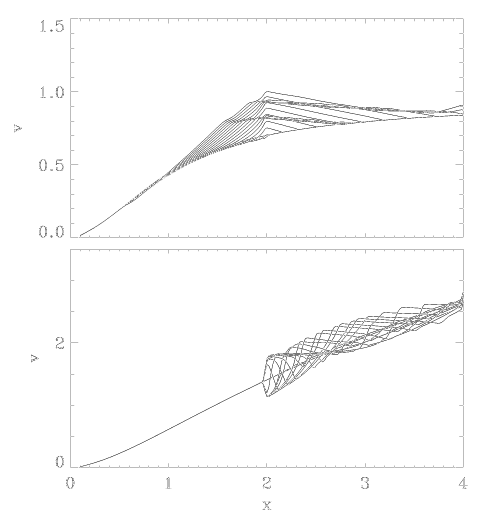
The critical wind is stable





Perturbation amplitude of 5% creates Abbott waves



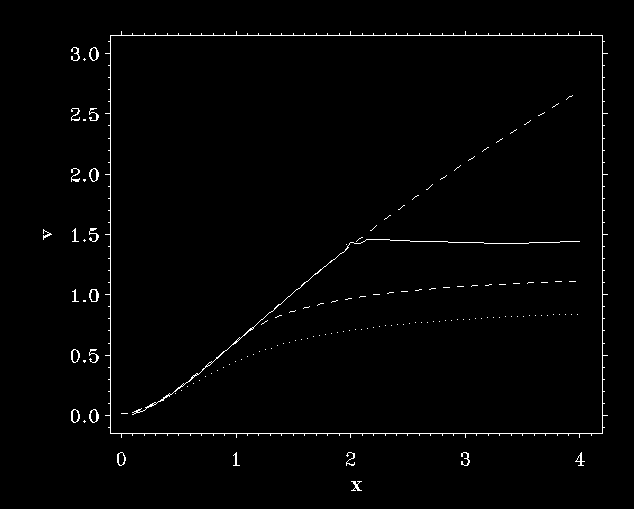
The same perturbation at 15% amplitude causes runaway


SOB



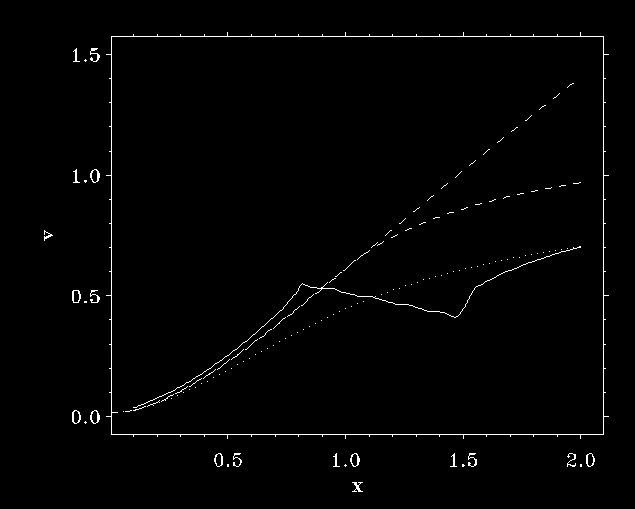
A perturbation below the critical point causes
stationary overloaded solution






Relevance of overloading?
blob infall
Howk & Cassinelli 2000 ApJ

Summary

0. Line force: SOB and SSF

1. Wind instability and X-ray emission

2. Accretion disk winds: without and with B field

3. Abbott waves and wind runaway

FIN