Dark corners in radiating fluids -

critical points, Abbott waves, & scattering



Achim Feldmeier
University Potsdam, 11 June 2001



This talk can be found at
http://www.astro.physik.uni-potsdam.de/~afeld









MOTIVATION: WHY ABBOTT WAVES?



Abbott waves are the fundamental wave mode in radiative flows (Abbott 1980, ApJ). They establish the information channel between infinity and the wind base.
Abbott waves shape the flow by mediating the evolution to the critical solution (cf. Laval nozzle or solar wind). Possible observational evidence for Abbott waves is given by DACs (discrete absorption components)





from Prinja & Howarth 1988, MNRAS



Unique feature: correlation with rotation period: Prinja 1988, MNRAS





Recent data from Kaper, Henrichs, Nichols, et al. 1996, A&A Suppl.




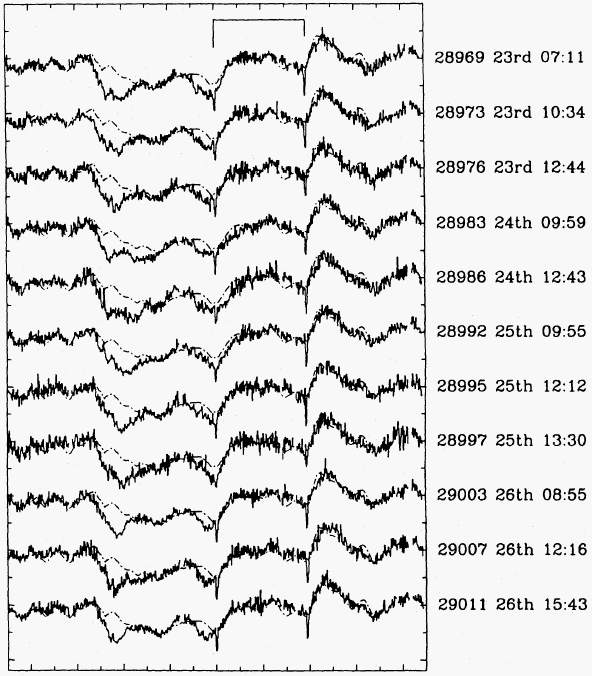
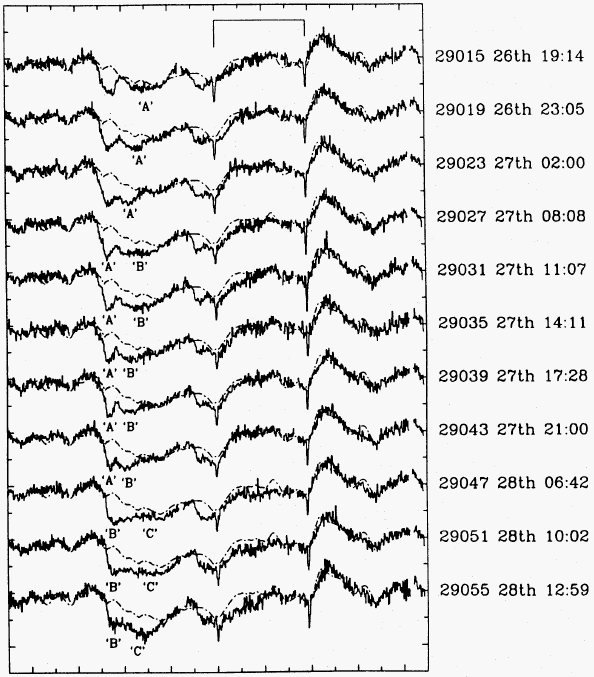
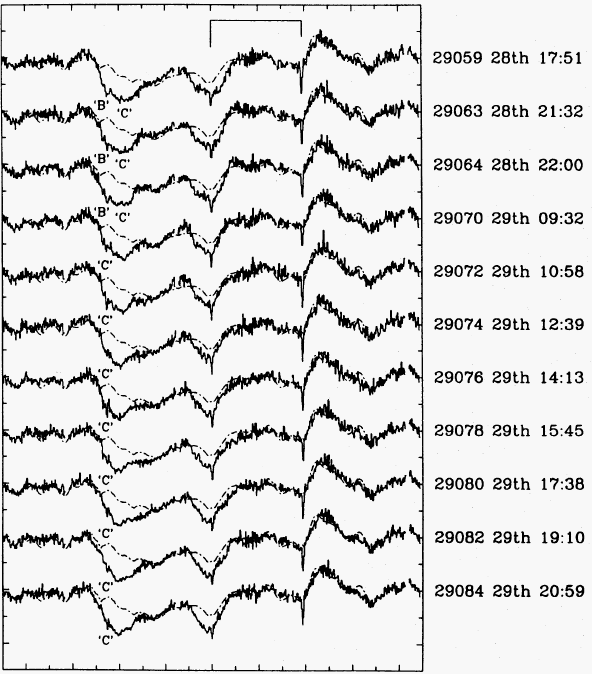
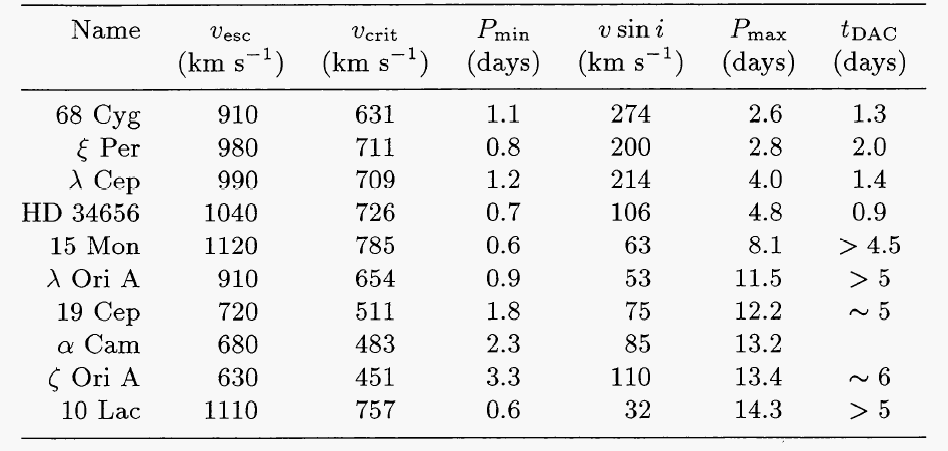
Explanation: corotating interaction regions, as in the solar wind ( Mullan 1984, ApJ)






azimuthal interaction between neighboring wind rays via Coriolis force is purely due to differing radial velocity laws.


From Cranmer & Owocki 1996, ApJ






Problem: recurrence time of CIRs is integer fraction (P/2 or P/4) of rotation period P. Recurrence time of DACs is similar to or longer than the rotation period.
Shallow velocity law as origin of DACs: Hamann 1980, A&A Shallow velocity law terminates in a kink. Abbott kink? Cranmer & Owocki 1996, ApJ













toomb
TOPICS TREATED IN THE FOLLOWING







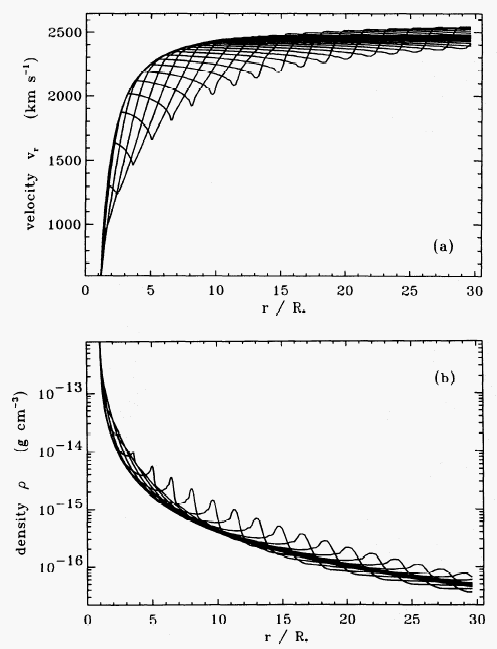
Please klick on the numbers. The floor plan is of the egyptian tomb of Niankhkhnum and Khnumhotep : http://www.egyptology.com/niankhkhnum_khnumhotep/floorplan.html















1

SELF-EXCITED WAVES






Owocki,Castor, & Rybicki 1988, ApJ



Numerical simulation of de-shadowing instability

for a flow driven by pure line absorption (no scattering).


Even without explicit perturbation at the wind base, ``there remains a train of nearly periodic self-excited waves.''


Explanation of this effect was given in Poe, Owocki, and Castor 1990, ApJ.
Use constant time step instead of constant Courant number:







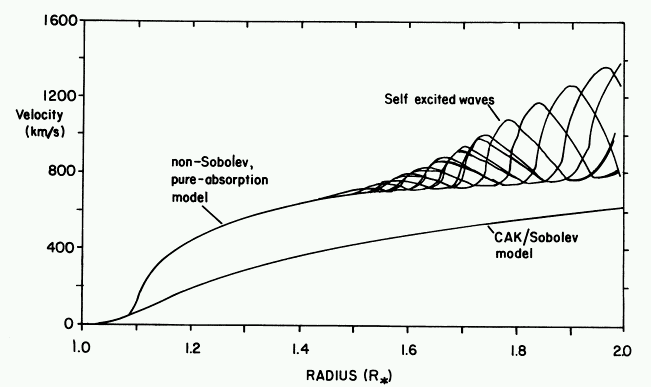
2

NO ABBOTT WAVES FOR PURE LINE ABSORPTION




Owocki and Rybicki 1986, ApJ:

study wind response to localized perturbation:

Green's function.


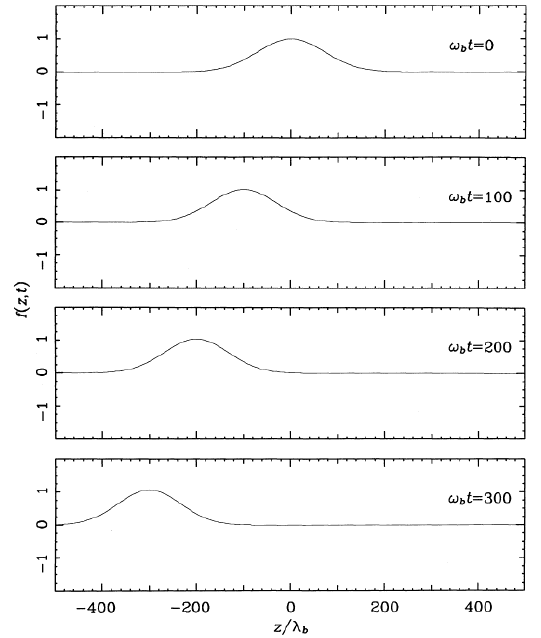Upstream propagation of a smooth Gaussian pulse as an Abbott wave
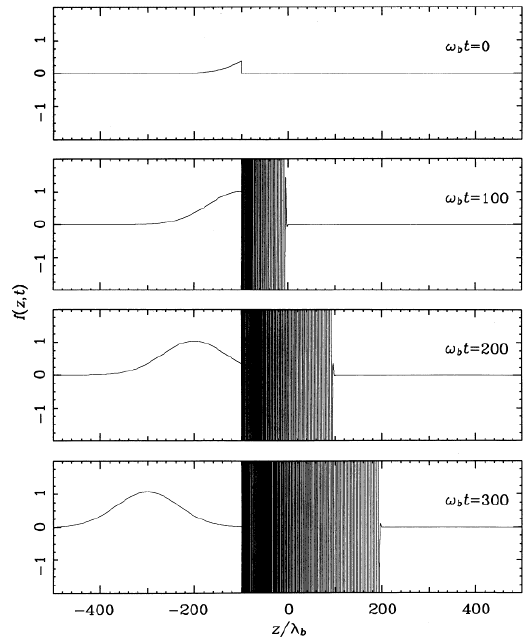Reconstruction & propagation of the full Gaussian from a truncatedone
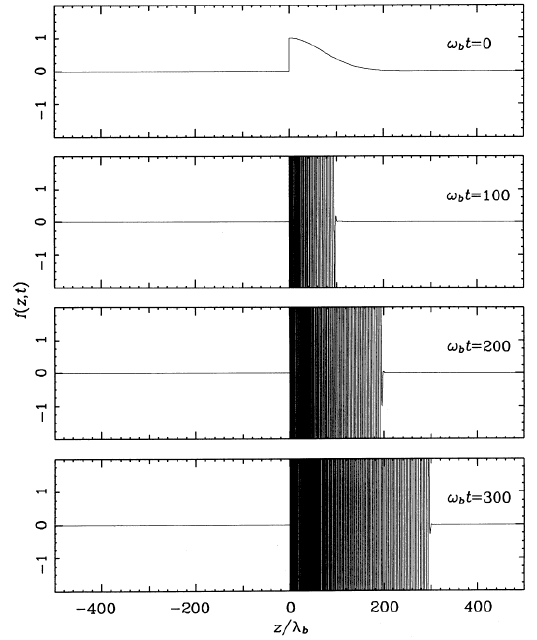Reconstruction occurs only upstream of the localized perturbation






BUT The O-R analysis is for pure absorption line driving.

In this case, it is obvious that no radiative wave propagates upstream. Hence, that no Abbott waves occur but only sound.

Missing is a Green's function analysis including scattering Has so far resisted all mathematical attempts




Owocki & Puls 1999, ApJ

Numerical Green's functions for Sobolev force, SSF (Sobolev source function), and EISF (escape integral source function) methods.




3

STEEP OCR SOLUTION










No base perturbation (OCR).







For explicit base perturbation (sound wave), the velocity law still jumps to the new, steep branch at r=1.1.



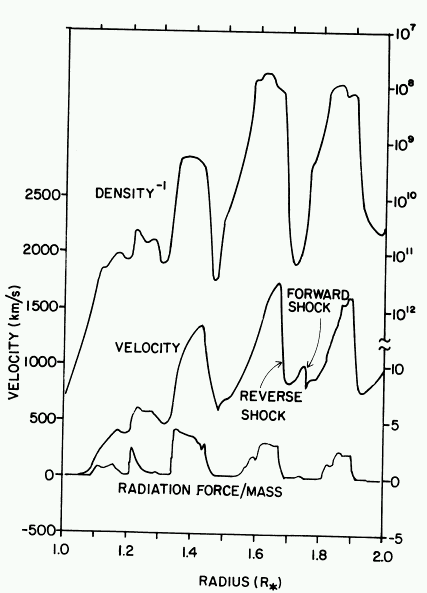
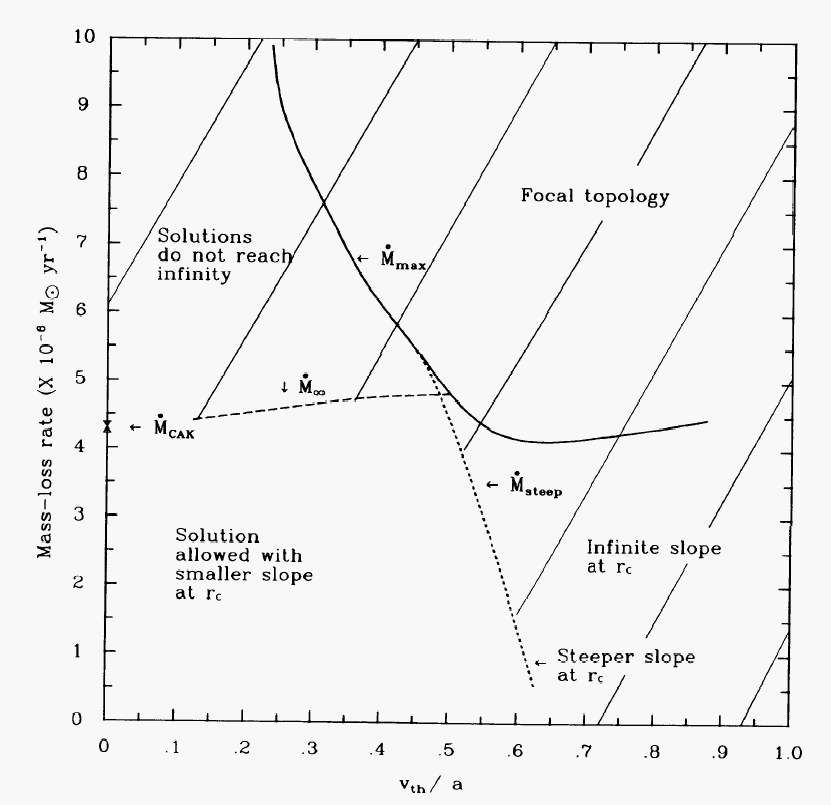
To safe computational costs in resolving the thermal width of a line profile... ...OCR assumed (i) large wind temperature and (ii) large ratio 1/2 of thermal-to-sound speed.
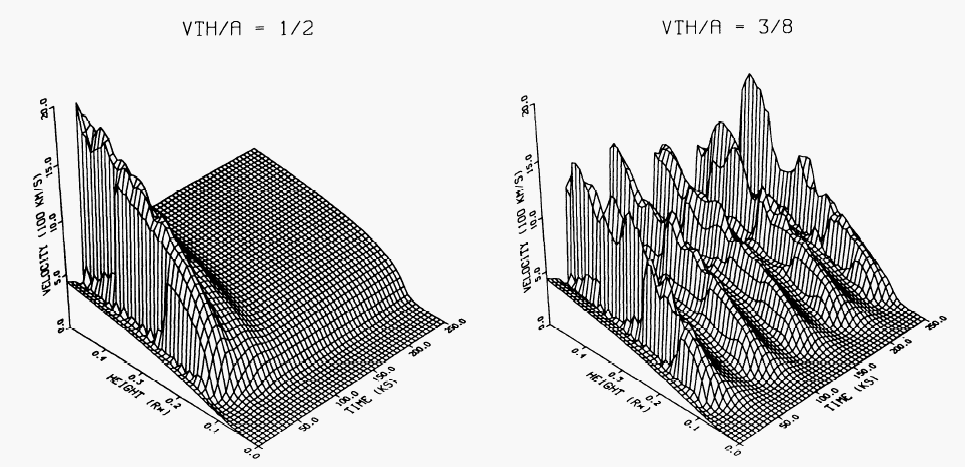
Assuming a physically more realistic ratio of 3/8, the models no longer jump to a steep solution... ...instead they become intrinsically time-dependent.





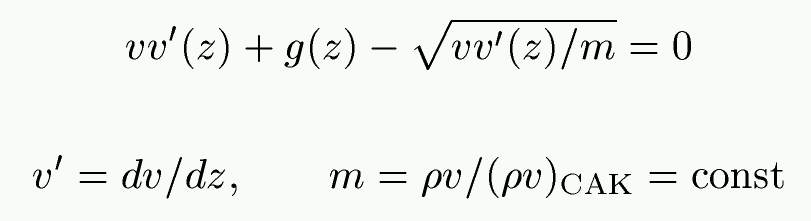
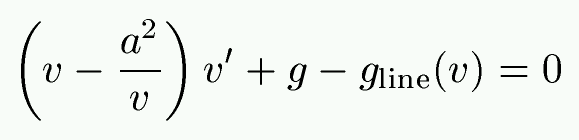
In Sobolev approximation, the 1-D, planar, stationary wind Euler equation for zero sound speed and CAK parameter alpha=1/2 is



For pure absorption instead of Sobolev approximation, and including a constant, non-zero sound speed , a, this becomes





Trivial: In the zw' plane, the former equation has a saddle point at the CAK critical point. Poe, Owocki, & Castor, 1990, ApJ: In the zv plane, the latter equation has a nodal point at the sonic point.
Note: these authors lost trust in the CAK critical point, believing that Abbott waves were gone (Owocki & Rybicki 1986, ApJ)




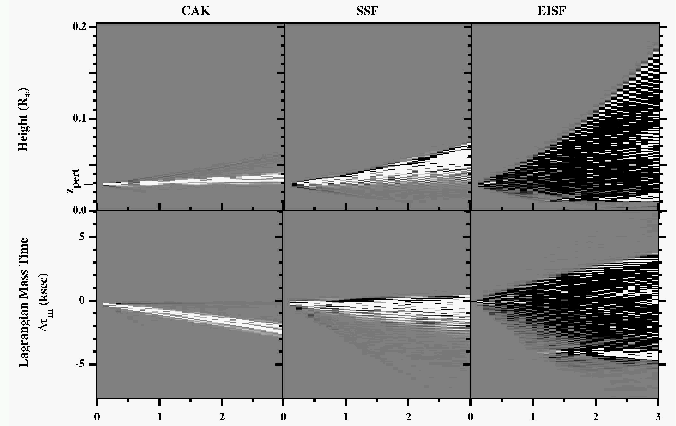
4

NODAL POINT TOPOLOGY






Saddle (left)
and
nodal point (right)


The existence of a second,
positive slope at v=a
in non-Sobolev models
is still not understood.

In Sobolev models, there is
only one positive slope at v=a (see CAK)



The new, steep slope
exists only in a narrow interval of
artificially high thermal speeds

Poe et al. 1990




--> SOLUTION DEGENERACY:


from Poe et al. 1990:



or:



from Owocki & Zank 1991:



or:



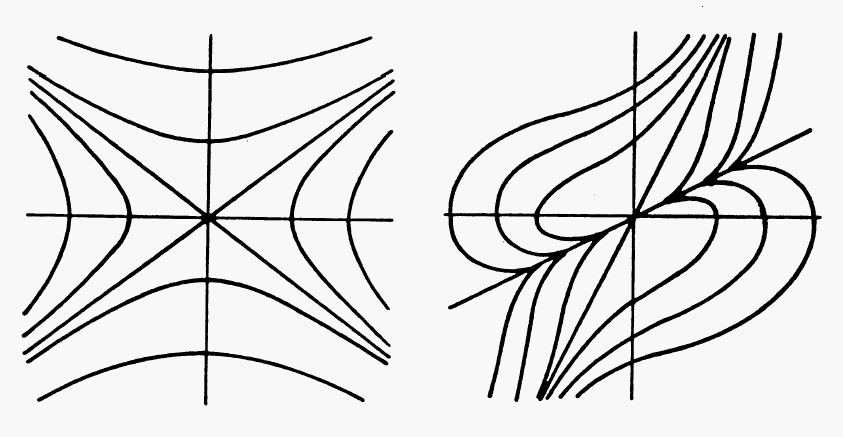
Poe et al.
and
Owocki & Zank:
nodal point explains solution degeneracy. 		My viewpoint:
nodal point topology shows that CAK (Abbott) point and not sonic point is relevant critical point.




5

VISCOSITY (POSSIBLY: RADIATIVE)



At any nodal point (in coronal, magnetic, radiative winds), viscosity repels converging solutions, hence viscosity breaks degeneracy (Owocki & Zank 1991, ApJ).




The unique solution
which passes from the
photosphere through the
viscous node to infinity
must be fine tuned
up 15 digits


But should viscosity not be very small and unimportant? Yes, but radiative viscosity may be large:




Note: when v'' is included in Sobolev approximation,
the de-shadowing instability appears (Feldmeier 1998, A&A):
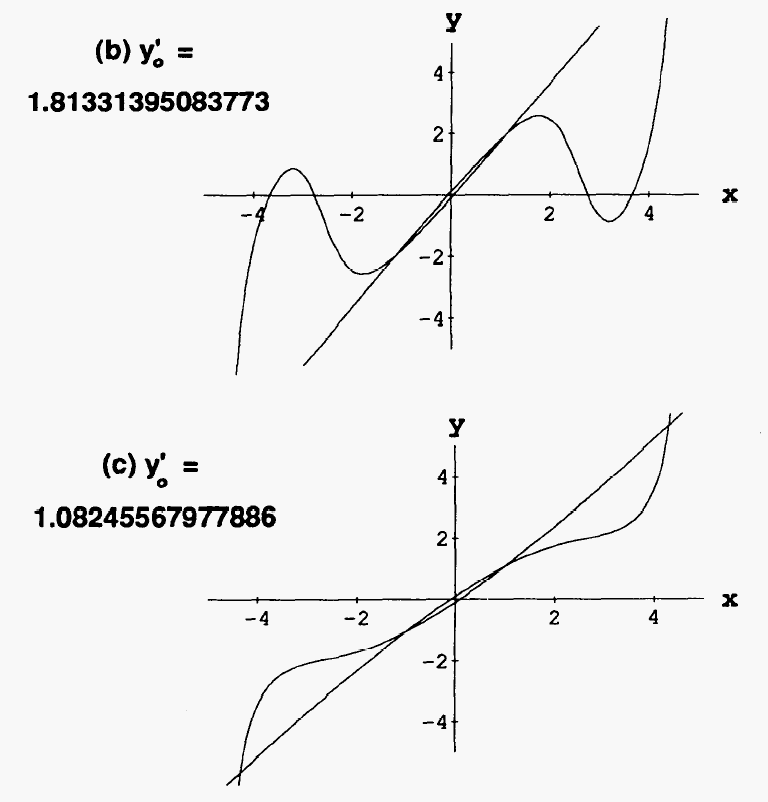
Abbott waves: v' Instability: v''




6

THE INFLUENCE OF SCATTERING



General conclusion: pure absorption case is degenerate limit,
both with respect to Abbott waves and nodal point topology.

More details ... in the lecture.

Relevant papers:

Owocki 1990 (Trieste)
Owocki & Puls 1996, ApJ (analytical)




7

ABBOTT WAVE RUNAWAY



Positive velocity slopes propagate upstream, negative slopes propagate downstream (F&S 2000, 2001a,b, ApJ).
Asymmetric evolution of v(r) towards larger speeds if dv/dr<0 occurs.
A perturbation amplitude of 4% gives stable Abbott wave propagation upstreams Rising the amplitude to 8% causes Abbott wave runaway via negative dv/dr





A sawtooth perturbation at x=2 with small amplitude creates upstream &inward propagating Abbott waves, but causes no runaway.



Doubling the perturbation amplitude causes runaway.





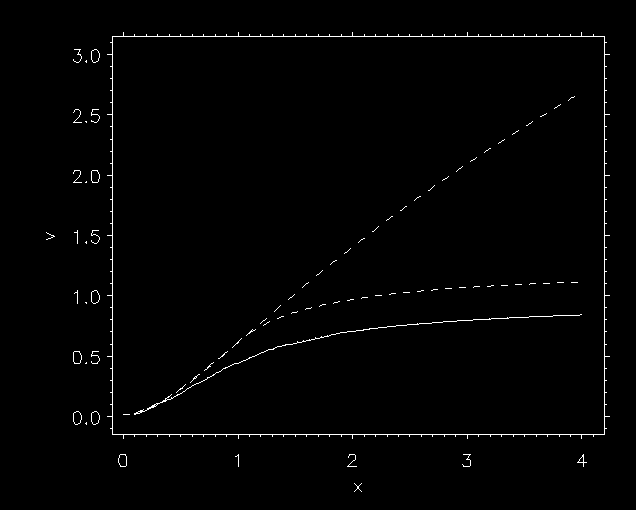
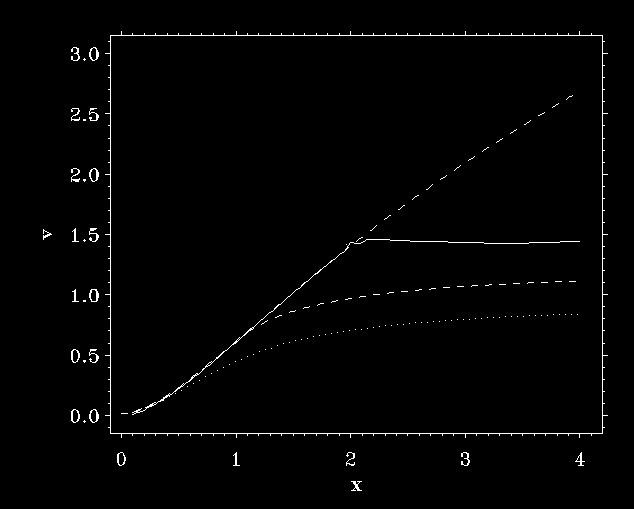
8

SHALLOW SLOPES VS ION RUNAWAY



Springmann & Pauldrach 1992, A&A: in thin winds from B main-sequence stars, radiatively driven ions may decouple from passive H plasma.

Bürgi 1992, J. Geophys. Res.: in the solar wind, H and He do NOT decouple. As so often, the analogy between coronal and radiative winds proves fruitful:

Krticka & Kubat 2000, A&A: solving 1-D, stationary hydrodynamic equations for a CAK wind using a Henyey (!) scheme, assuming `Chandrasekhar' friction between H and metals, they find:






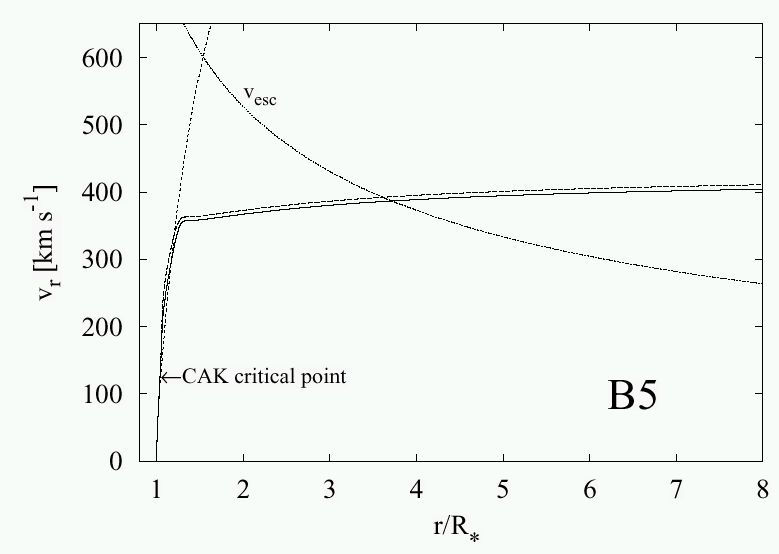
No decoupling! Passive H plasma and radiat. driven metals... ...adopt a shallower (no shallow?) velocity law.


Basic question is again for g_line(v) vs g_line(v'):



These results for an isothermal wind.

If energy equation is included:

heating -> lower g_line -> lower v_inf.

Krticka &Kubat 2001, A&A




LAST WORDS



Our major topics were the interplay of

critical points Abbott waves
v, v', v'' scattering