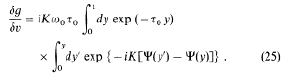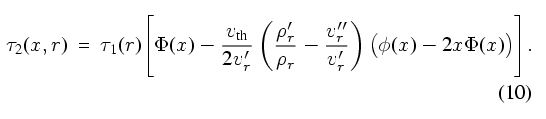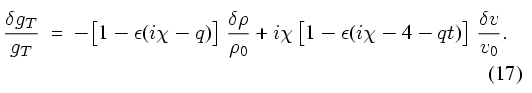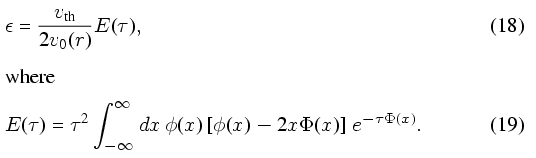(c) Philip Gibbs
http://www.public.iastate.edu/~physics/sci.physics/faq/light-mill.html
LightMill image and animation by Torsten Hiddessen
|
Particles |
|
p=mv=2E/v |
|
Photons |
E=hn
|
p=E/c |
|
| History of (radiation driven) stellar winds
|
|
Wolf & Rayet
|
1867
|
class of stars with very broad spectral lines
|
|
Milne
|
1926
|
new plasma instability in the solar chromosphere
|
 |
Beals
Chandrasekhar
|
1929
1934
|
broad emission lines from W-R stars form in continuous outflow
|
|
Parker
|
1958
1960
|
hydrodynamics (!) of transonic (!) solar wind
|
|
[space borne UV spectrographs]
|
1967
|
P Cygni lines from O stars
|
 |
Lucy & Solomon
Castor, Abbott & Klein
|
1970
1975
|
stationary wind theory via radiative line driving
|
|
Abbott, Hamann, Hillier, Hummer, Kudritzki, Lucy, Owocki,
Pauldrach, Puls, Rybicki
|
1980 - now
|
complex radiative transfer and non-LTE wind models
including >100.000 lines, atmospheric blocking, multiline
processes,...
|
 |
|
Begelman, Norman, Shlosman, Turnshek, Weymann
|
again 1980 - now
|
radiation driven winds from accretion disks
in quasars, cataclysmic variables, & young stellar objects
|
 |
| Recent interests in line driven hydrodynamics
|
 |
Shocks from the line driven instability
Owocki et al. 1988 ApJ |
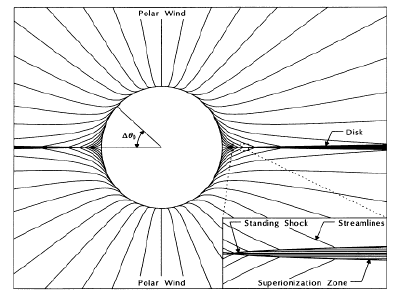 |
Wind compressed
disks Bjorkman & Cassinelli 1993
ApJ |
 |
Corotating
interaction regions Cranmer & Owocki
1996 ApJ |

|
High-mass X-ray
binaries Blondin et al. 1990 ApJ
|
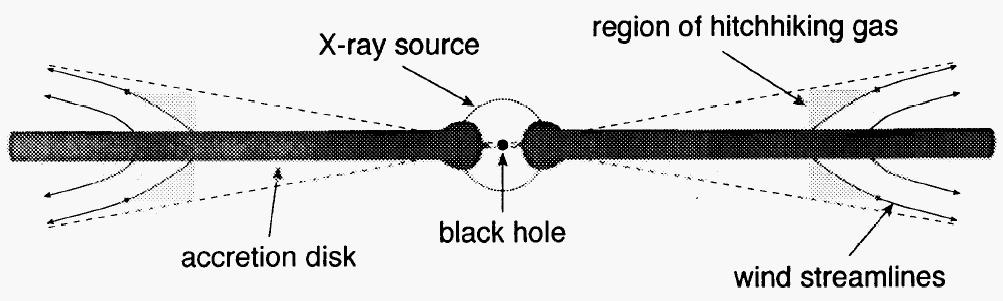
|
Quasar winds
Murray et al. 1995 ApJ |

|
Disk winds Feldmeier & Drew 2000 MNRAS |
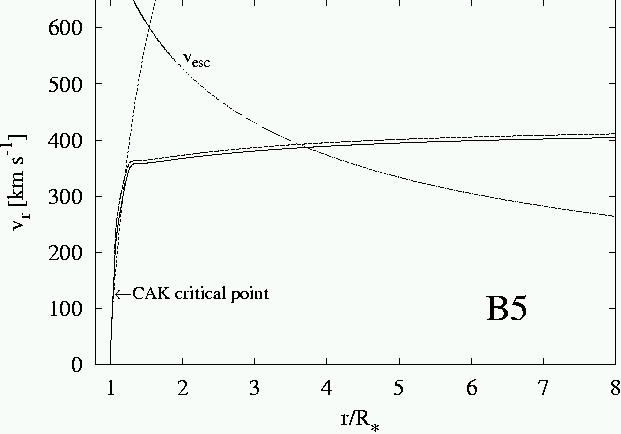
|
Thin winds Krticka & Kubat 2000 A&A |
For a planar, one-dimensional wind
at zero sound speed,
the continuity and Euler equations become
in Sobolev approximation,
assuming a CAK line distribution
(F the stellar flux, C force constant, 0 < alpha < 1):
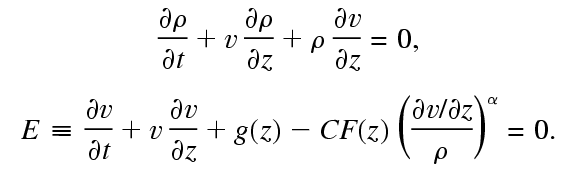
| Hydronumerics of the CAK solution |
Fortran hydrodynamics code for
solar wind and
radiation driven wind after CAK

The non-linear appearence of dv/dz
makes line driving almost as rich
as the Lorentz force in MHD
Especially, a new wave type occurs:
Abbott waves
And a new type of instability:
de-shadowing instability
(back to start)
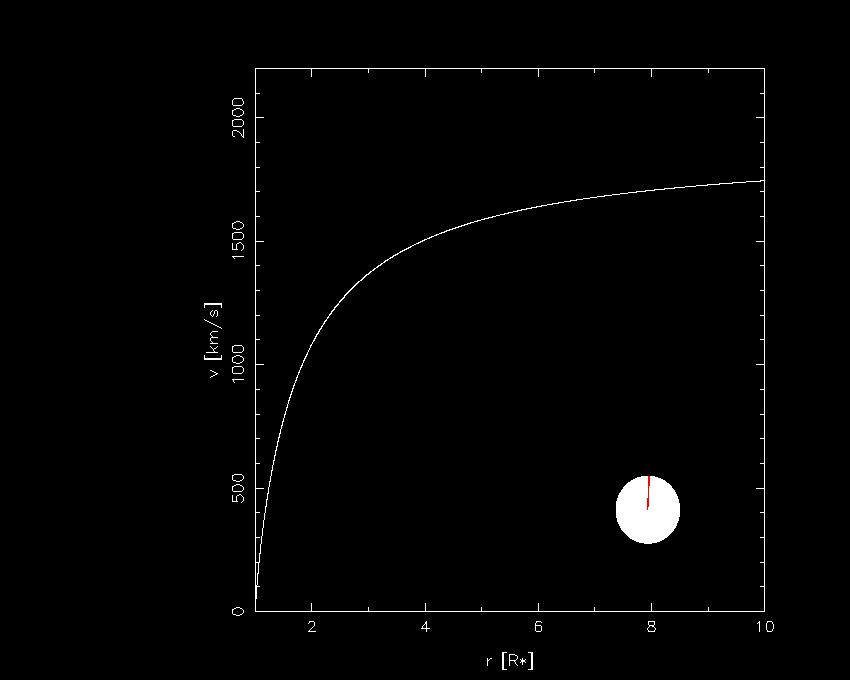 (Please klick on the image)
(Please klick on the image)
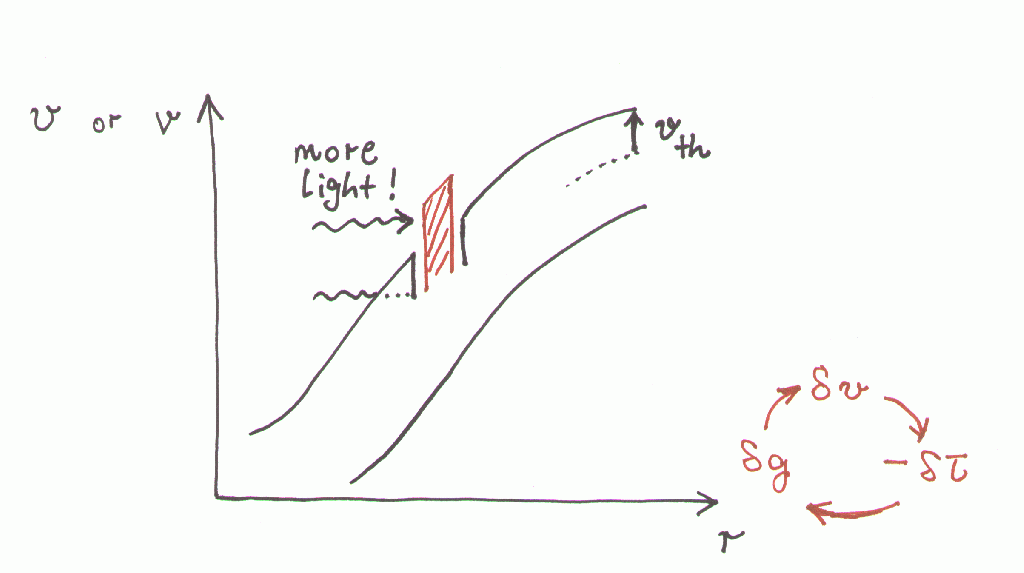
Consider a
short scale perturbation which accelerates a fluid parcel to
larger speeds. The perturbation gets amplified, since the parcel sees
more stellar light ("unshadowing") and experiences a larger line
force, which accelerates it further. This is the line driven
instability.
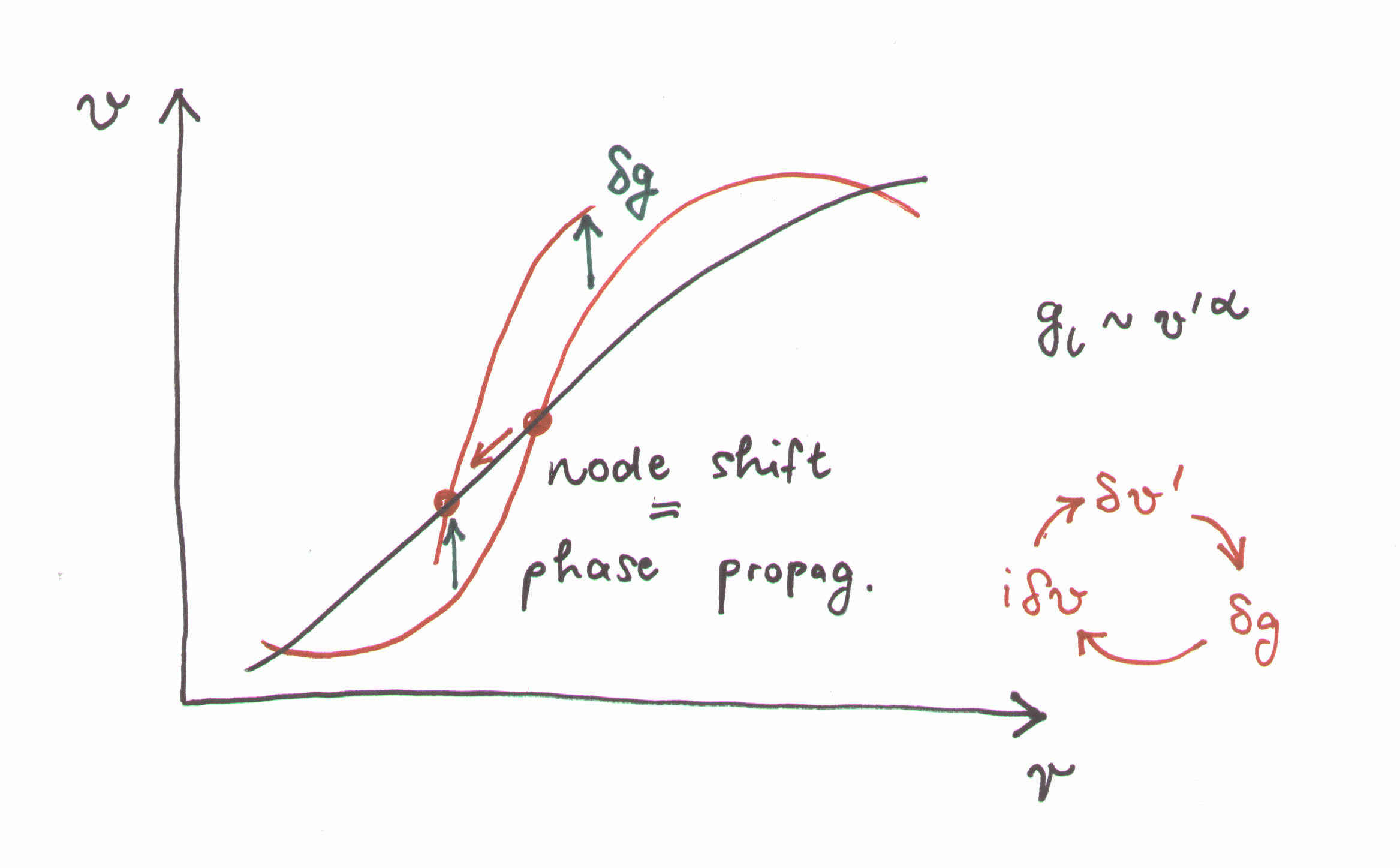
Consider a
large scale perturbation of the wind velocity law. At the
node where the velocity gradients steepens, the Sobolev line force
increases. The gas is accelerated to larger speeds ("upwards"), hence
the node shifts inwards. This corresponds to an inward phase
propagation, or a (marginally stable) Abbott wave. The same occurs at
a node where the velocity law becomes shallower.
| Unshadowing instability of thermal
band: short wavelength limit (Lucy & Solomon 1970 ApJ) |
| Stable waves from 1st order Sobolev:
long wavelength limit (Abbott 1980 ApJ) |
|
Bridging law from exact (!) line transfer (Owocki & Rybicki
1984 ApJ) |
Unstable waves from 2nd order Sobolev (Feldmeier 1998
A&A) |
|
|
|
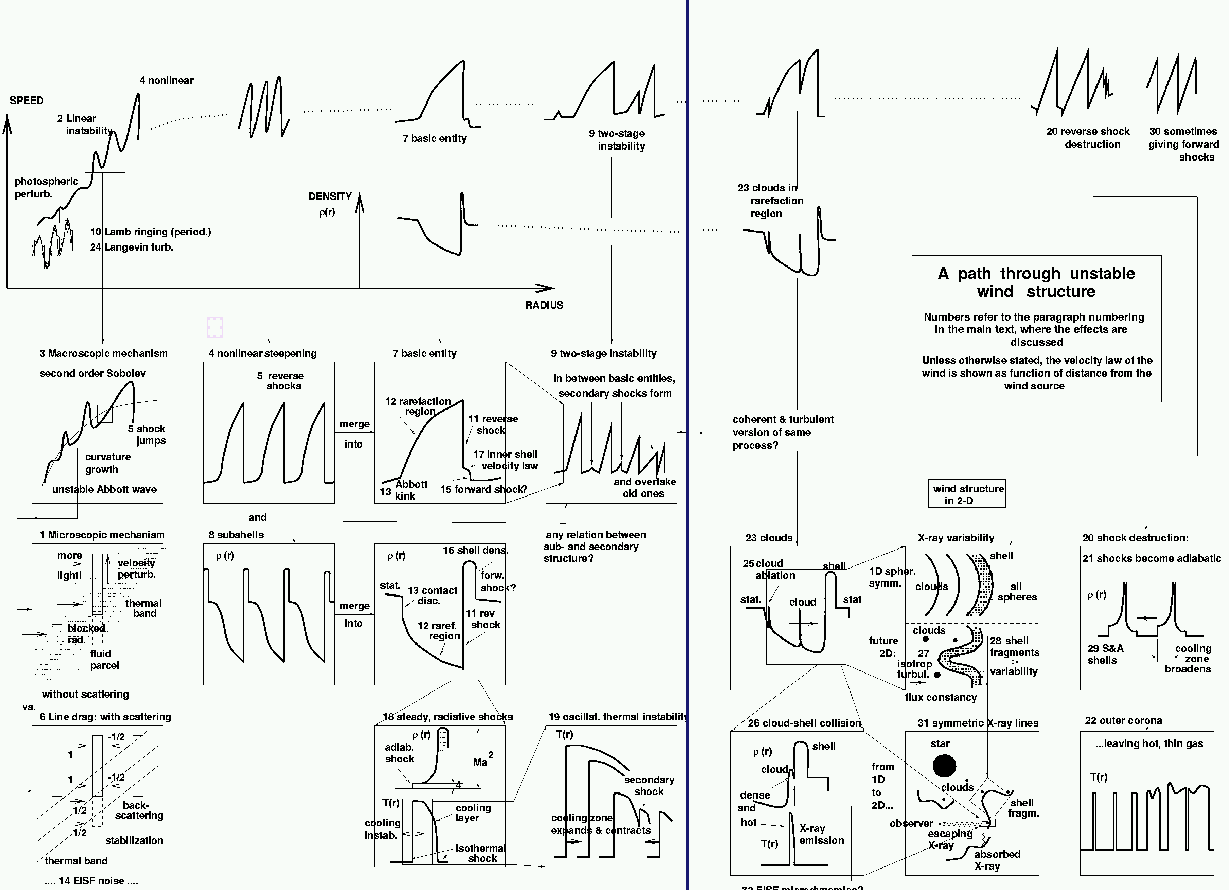
Up to now, four formulations of the line driving force gl
were given, of increasing complexity:
|
Sobolev force (simple)
|
SOB
|
Abbott waves, wind runaway
|
|
Pure absorption (complex)
|
ABS
|
Wind instability
|
|
Smooth source function force (complex)
|
SSF
|
Wind instability
|
|
Ensemble integrated source function force (very complex)
|
EISF
|
Instability, phase change, and Sobolev theory!
|
In general, an angle integral has to be applied.
For simplicity, we consider here only the force arising from radially
streaming photons
f:
Doppler line profile function
u: wind velocity, in units of thermal speed
x: normalized frequency, in Doppler units from line center
r: wind density
C: a constant
Sobolev force (Castor, Abbott, Klein
1975):
purely algebraic, on 50 spatial mesh points
|
gl = Cr-2 |
æ
è
|
r-1 du/dr |
ö
ø
|
a
|
, 0 < a < 1 |
| |
Pure absorption (Owocki, Castor,
Rybicki 1988):
double integral on 5000 spatial
× 50 frequency mesh points
|
gl = Cr-2 |
ó
õ
|
¥
-¥
|
dx |
|
|
é
ë
|
ó
õ
|
r
|
dr¢r(r¢) f |
æ
è
|
x-u(r¢) |
ö
ø
|
ù
û
|
a
|
|
|
| |
SSF (Owocki 1991):
double integral on 5000 spatial × 50
frequency mesh points
|
|
|
|
Cr-2 |
ó
õ
|
¥
-¥
|
dx f |
æ
è
|
x-u(r) |
ö
ø
|
|
æ
ç
è
|
|
1-S(r)
t+a(x,r)
|
+ |
S(r)
t-a(x,r)
|
|
ö
÷
ø
|
|
| | |
|
|
|
ó
õ
|
r
|
dr¢ r(r¢) f |
æ
è
|
x-u(r¢) |
ö
ø
|
|
| | |
|
| |
|
EISF (Owocki and Puls 1996):
four-fold integral on (5000 spatial × 50
frequency)2 mesh points
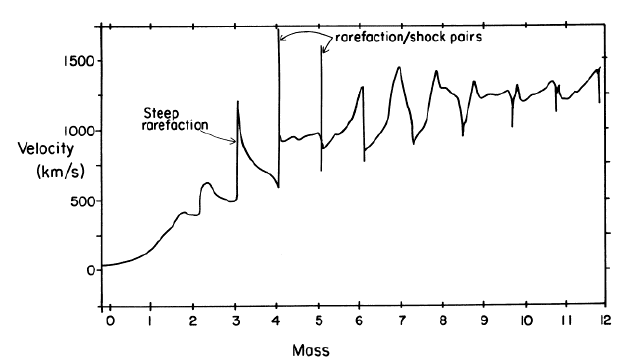
| Wind structure from numerical hydrodynamics
|
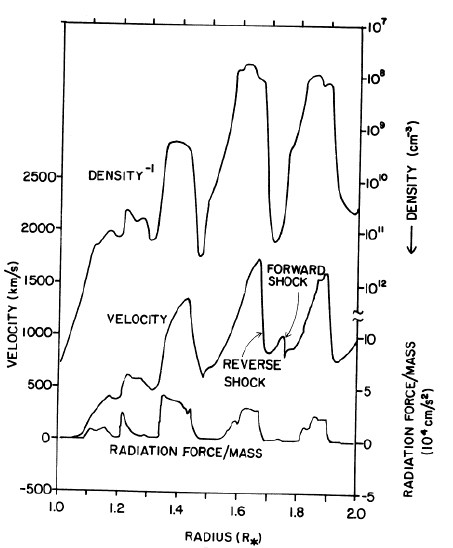
Owocki, Castor, Rybicki 1988 ApJ
ABS
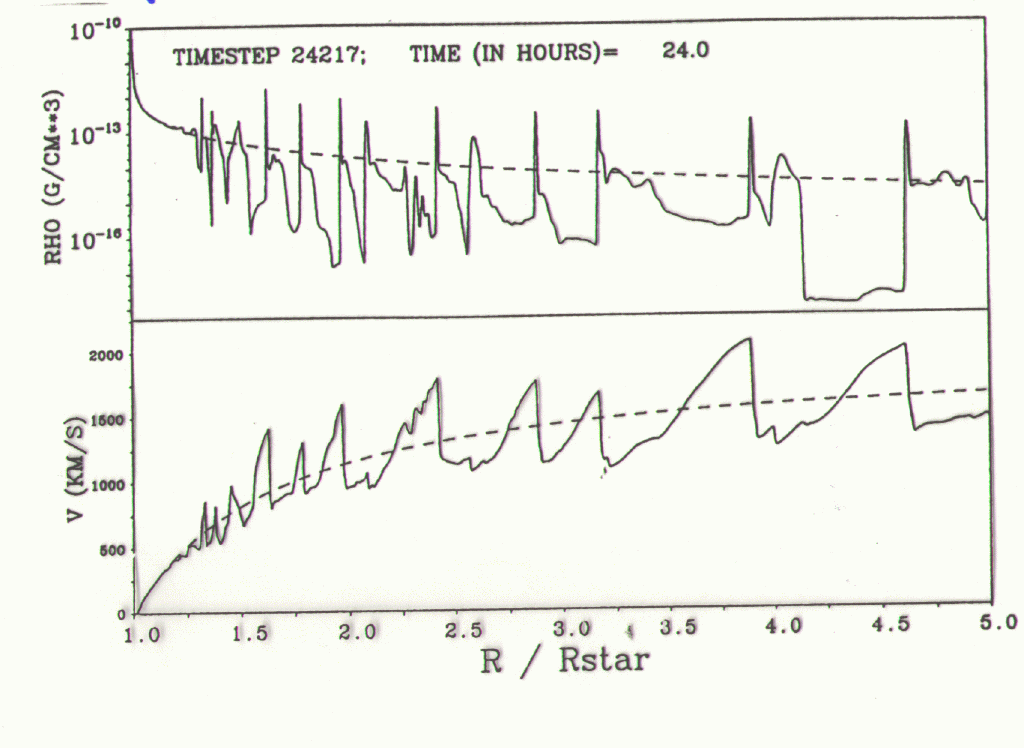
Feldmeier 1994 Ap&SS
SSF
The radial evolution of the wind
- from small radii, where perturbations are injected
- to large radii of fully developed structure
- to very large radii, where the structure decays
takes the form
- Broad rarefactions regions
- of optically thin gas
- being accelerated to large speeds
|
- Highly overdense shells (1-D simulat.)
- enclosed on inner side by starward facing reverse shocks
- which decelerate fast, rarefied gas
|
This structure is stable, since
- the rarefaction fins are optically thin
- and the gas in the shells decelerates
|
whereas the unshadowing instability requires
- optically thick AND
- accelerating gas
|
|
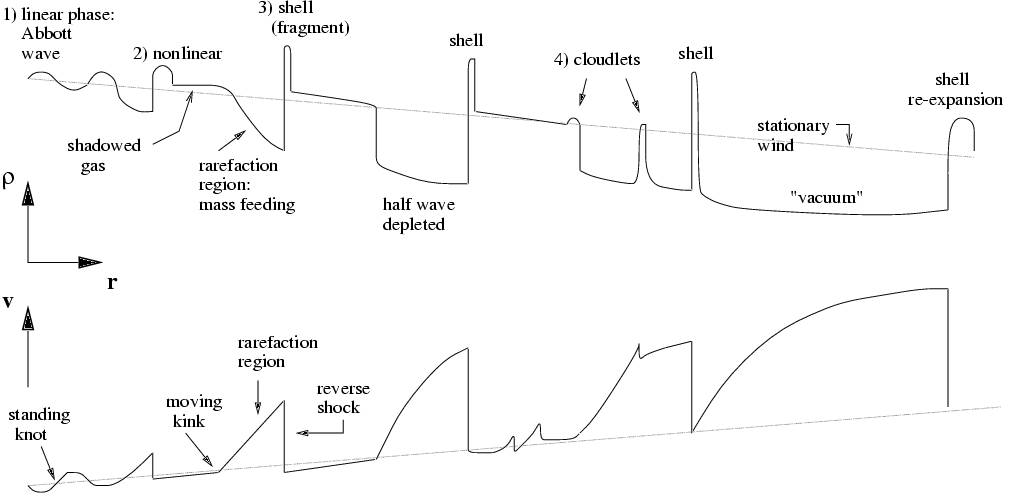
(back to start)
Owocki and Rybicki 1986:
Instead of dispersion analysis using sine waves
study wind response to localized perturbation:
Green's function.
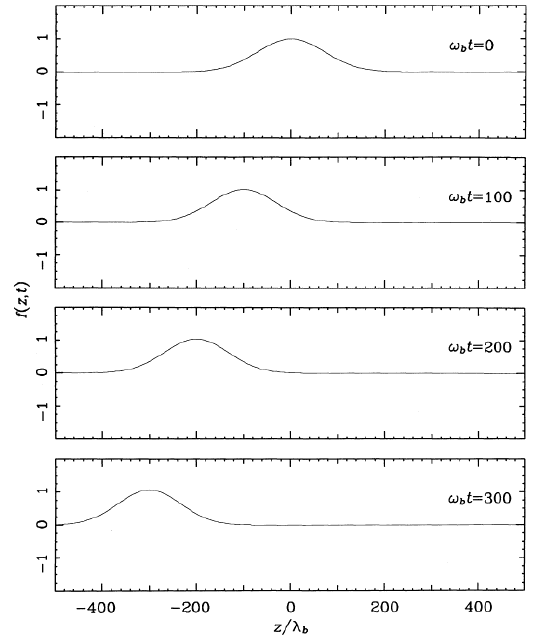 |
ABS
Propagation of a smooth Gaussian pulse as an Abbott wave |
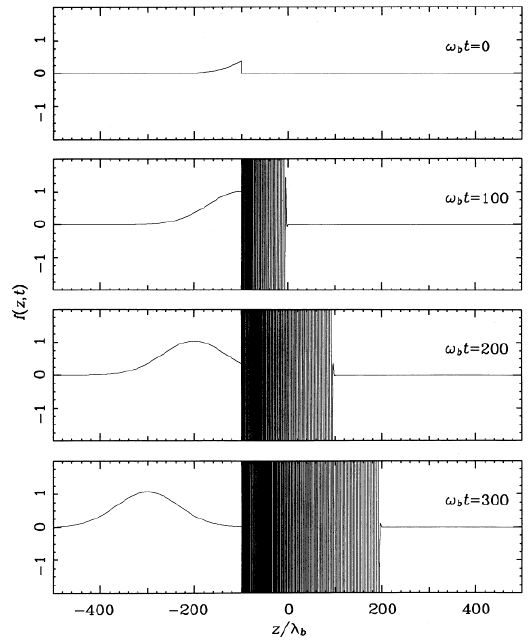 |
Reconstruction & propagation of the full Gaussian from a truncated one |
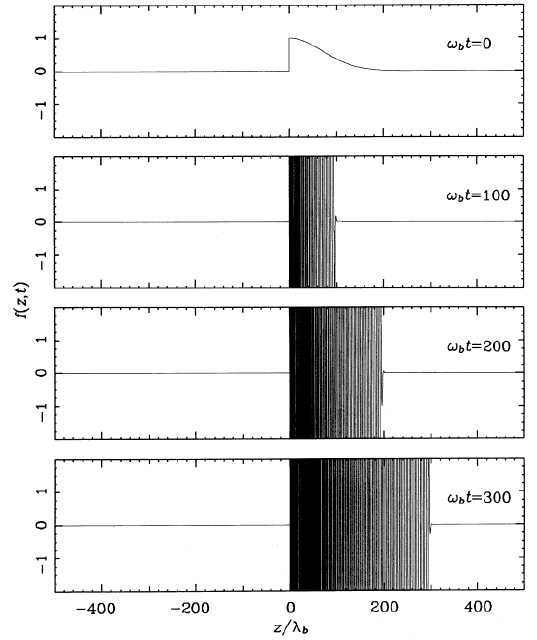 |
Reconstruction occurs only upstream of the localized perturbation =
discontinuity.
This truncated Gaussian vanishes upstream,
hence nothing propagates |
Information propagation?
BUT The O-R analysis
is for pure absorption line driving.
In this case, it is trivial that no
radiative wave propagates upstream. Hence, that no Abbott waves occur
but only pure sound.
Nobody knows so far what happens for scattering lines beyond the
Sobolev approximation...
(back to start)
Corona model ruled out:
- no K-shell absorption observed
(Cassinelli & Swank 1983)
- no green Fe XIV line observed
(Baade & Lucy 1987)
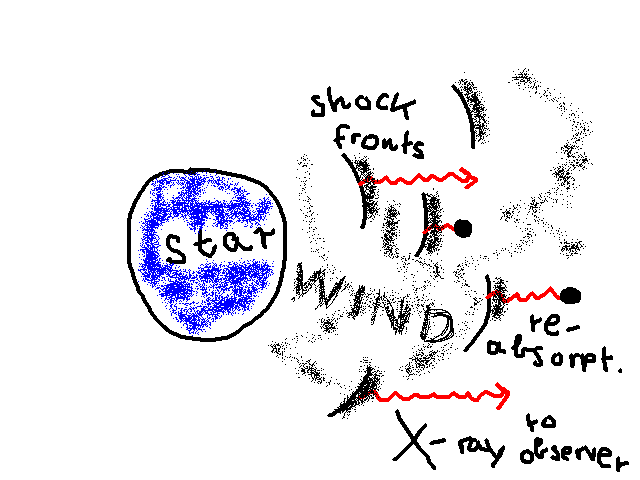 Favored scenario:
Favored scenario:
X-ray source embedded in the wind
Random shock fronts
(Lucy 1980
ApJ; Cassinelli & Swank 1983 ApJ; Hillier et al. A&A 1994)
| First problem with time-dependent wind models
|
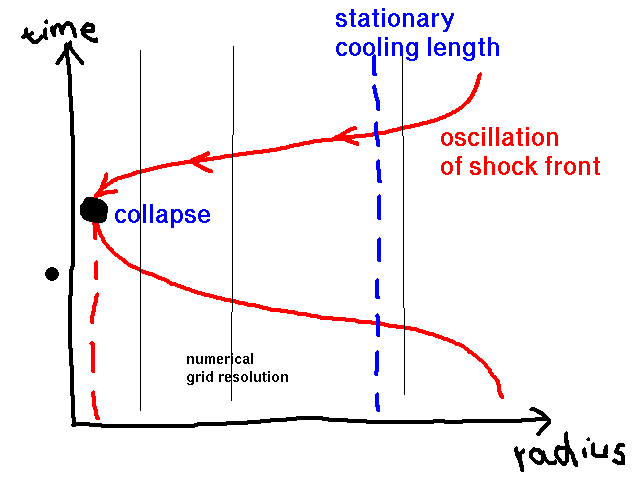 Strong oscillatory thermal instability
Strong oscillatory thermal instability
(Langer et al. 1981 ApJ; Chevalier & Imamura
1982 ApJ)
leads to collapse of cooling zone
on Eulerian mesh
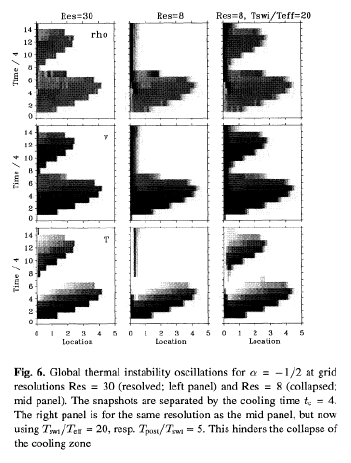
Way out: modify cooling function artificially to have
stable slope at low temperatures, irrelevant for X-ray emission
(Feldmeier 1994 Diss, 1995 A&A)
| Second problem with time-dependent wind models
|
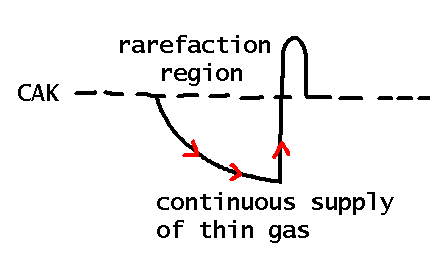
|
density too small. Not enough X-rays
(Hillier et al. 1994 A&A) |
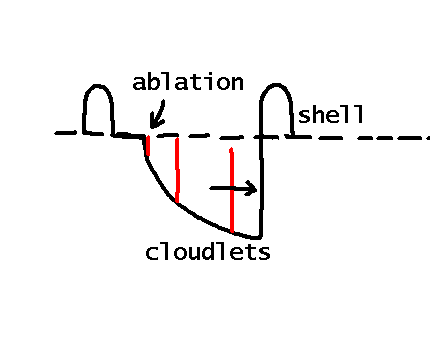
|
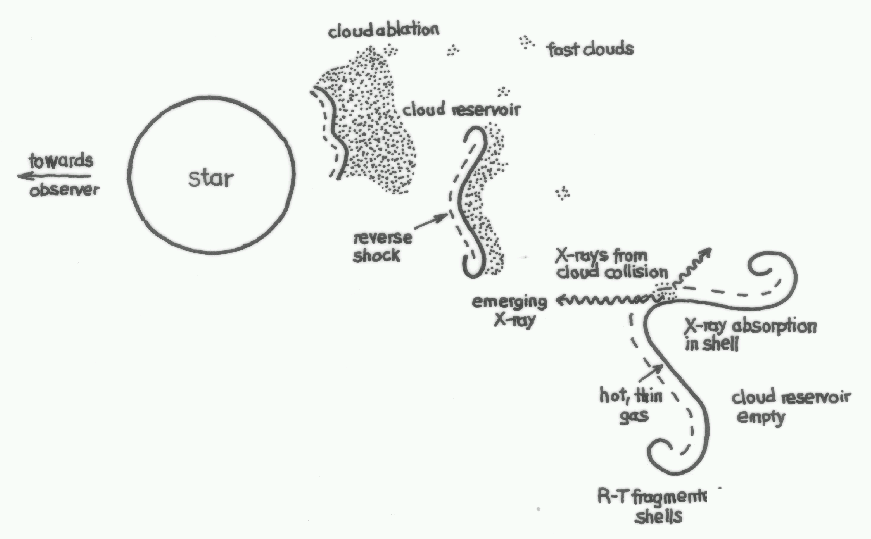
solution: we propose
(SSF)
fast & dense cloudlets collide with shells
(Feldmeier et al. 1997 A&A)
|
| Wind model for zeta Ori, including energy transfer
|
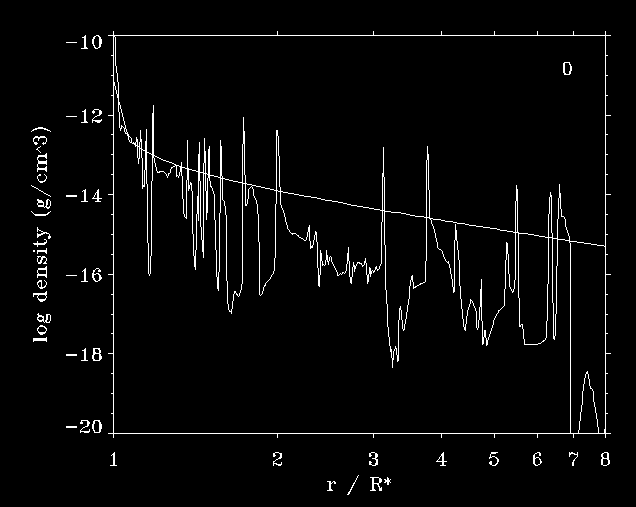
| Density, velocity and temperature snapshot at 3.5 days
after model start.
|
Synthesised X-ray spectrum from this snapshot, compared
to ROSAT data
|
The unique wind site responsible for this X-ray
emission
|
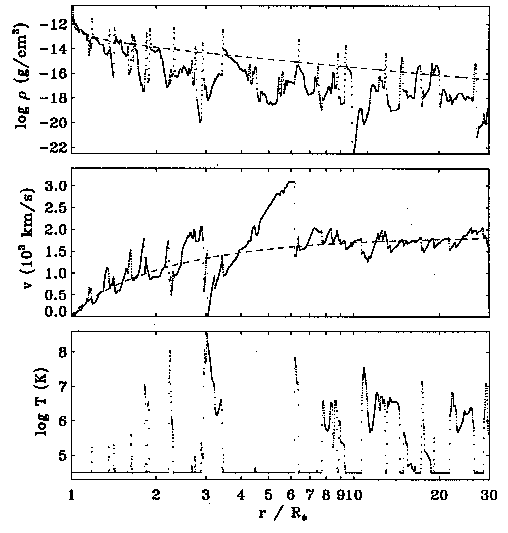 |
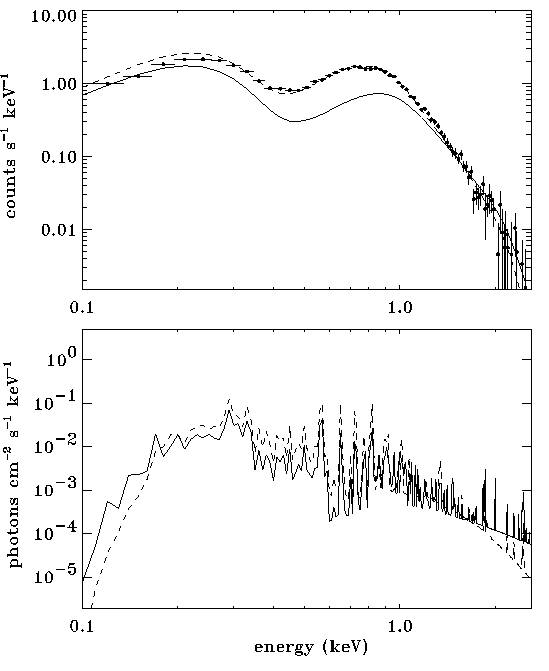 |
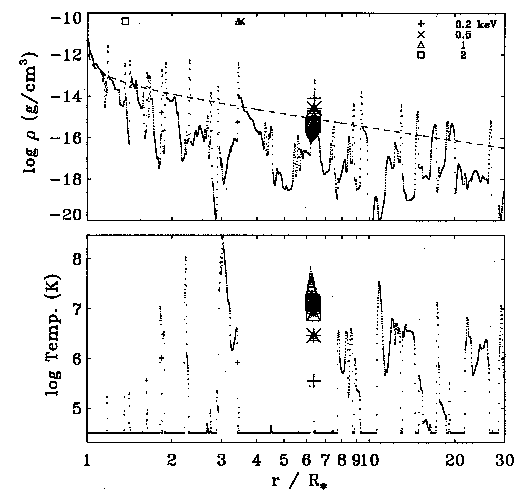 |
(Please klick on the
thumbnails for full-size images)
| Evolution of wind structure in time |
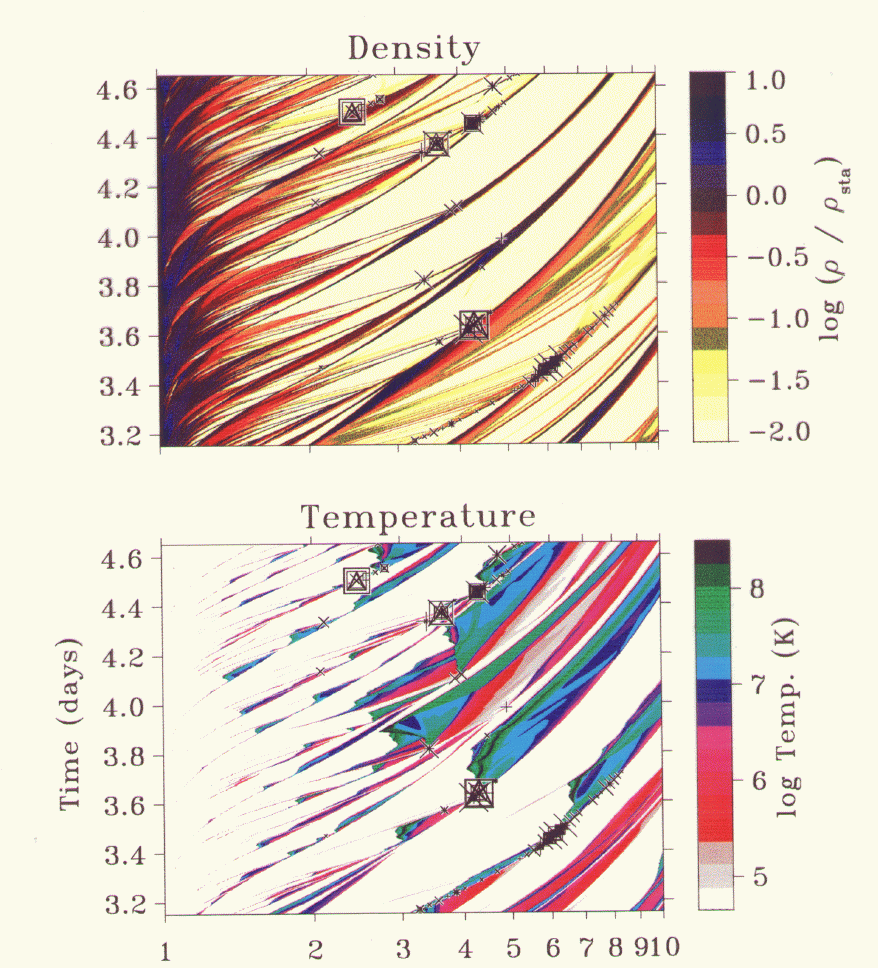
SSF
- Note numerous cloudlets in density plot
- ALL X-ray emission stems ONLY from cloudlet-shell collisions
- The snapshots above are at 3.5 days.
Note the cloudlet
collision between 6 and 7
stellar radii in the wind
evolution
(This movie file is too big for
net
transport: available only on home machine)
| X-ray lines with CHANDRA and XMM |
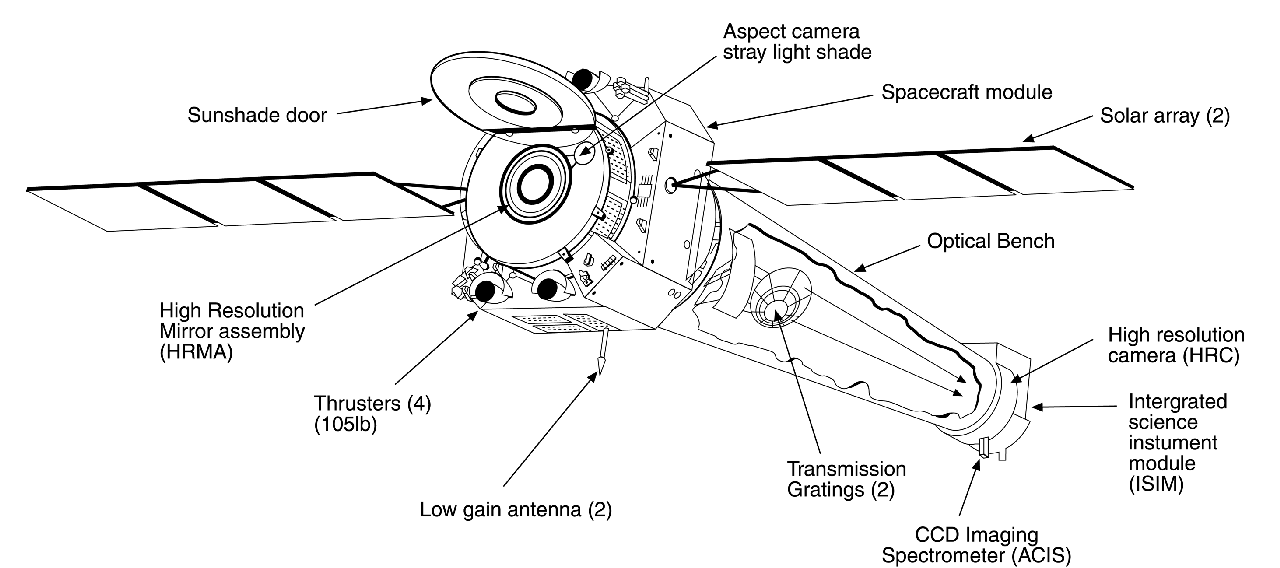
The CHANDRA satellite

The LETG grating is a freestanding gold grating
made of fine wires or bars with a regular spacing,
or period , of 1 micrometer. The fine gold wires are held by
two different support structures, a linear grid with
0.025 mm and a coarse triangular mesh with 2 mm
spacing. The gratings are mounted onto a toroidal
ring structure matched to the Chandra mirrors.
The LETG gratings are designed to cover an
energy range of 0.08 to 2 keV. However, their
diffraction can also be seen in visible light, which is
beautifully shown in the picture above right.

The CCD chip array with X-ray spectrum


XMM mirror, 3/4 (left picture) and fully (right picture)
assembled
Application of X-ray CCDs in medicine:

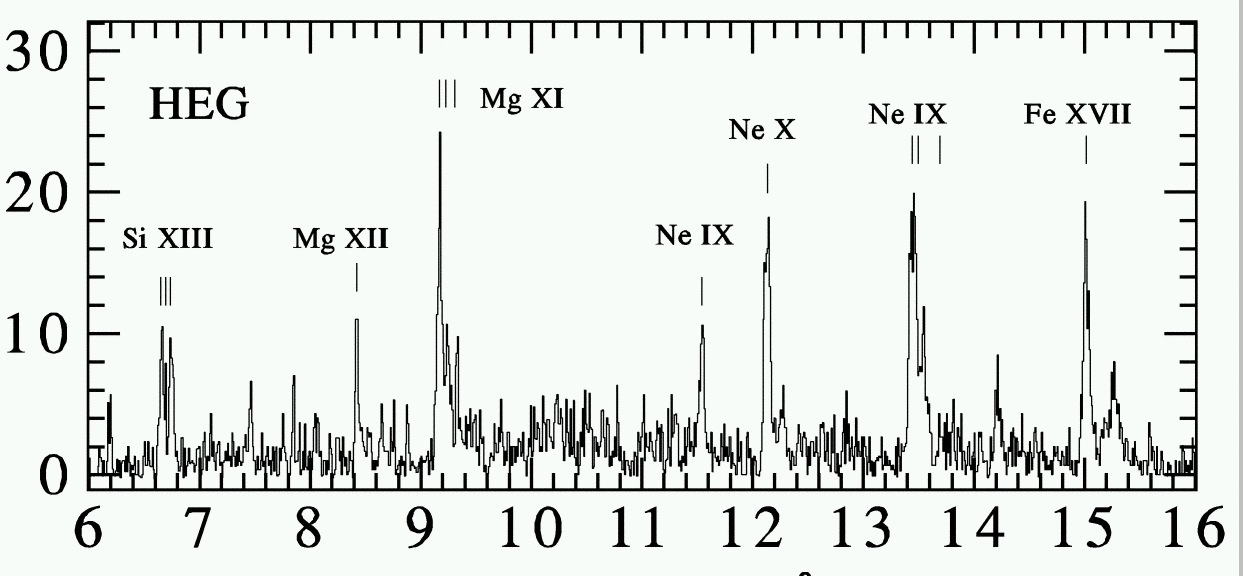 |
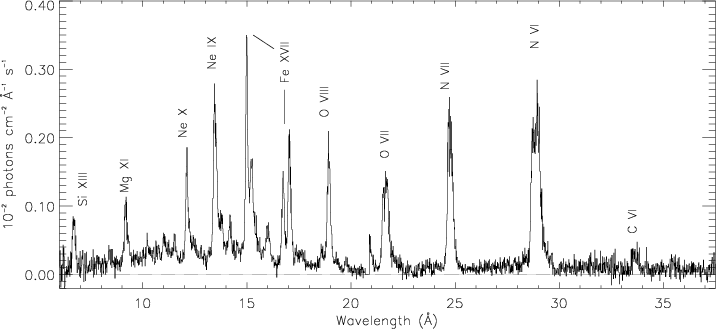
CHANDRA: zeta Ori
Waldron & Cassinelli 2001 ApJ
counts vs. Angstrom
|
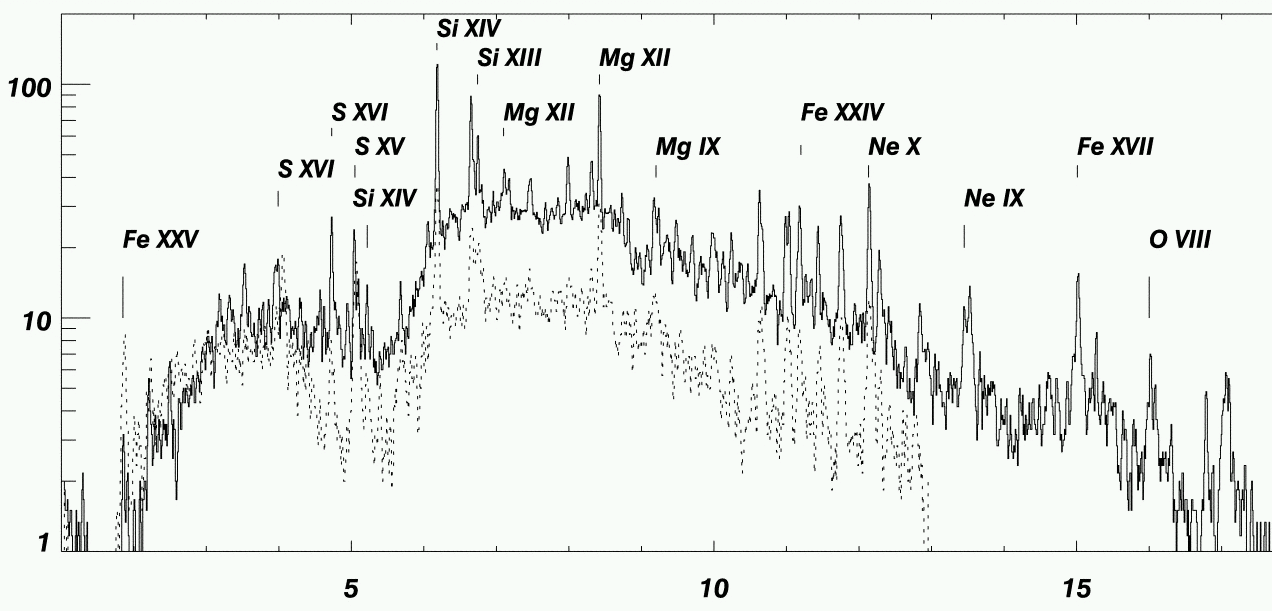 |
CHANDRA: Theta 1 Ori C
Schulz et al. 2001 ApJ
|
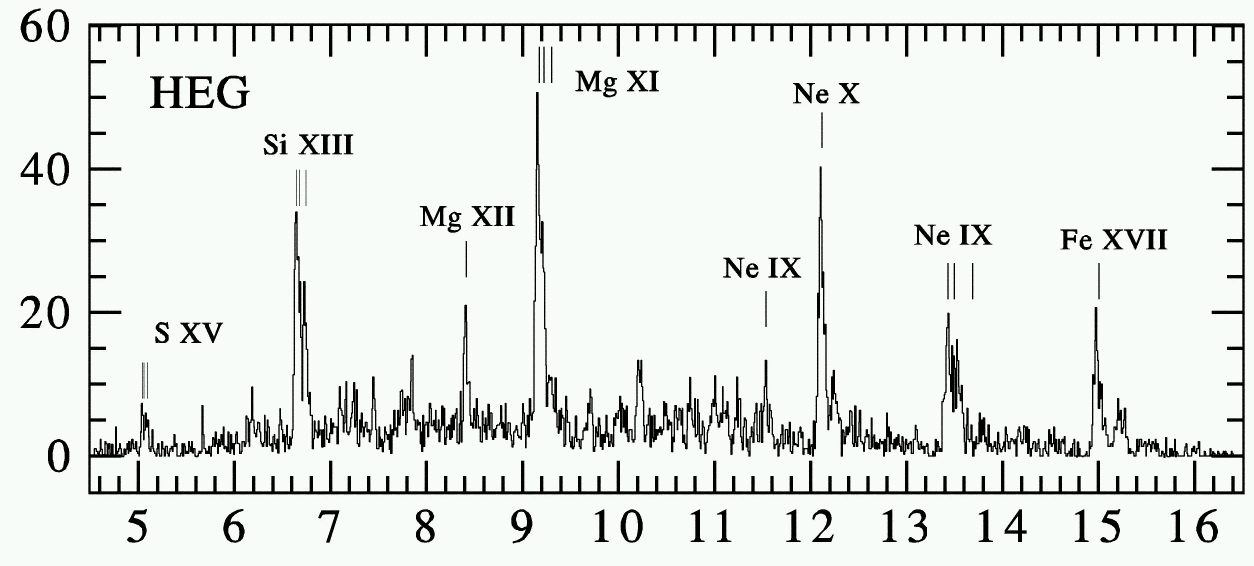 |
CHANDRA: zeta Pup
Cassinelli et al. 2001 ApJ
counts vs. Angstrom
|
 |
XMM: zeta Pup
Kahn et al. 2001 A&A
|
From Cassinelli et al. 2001, ApJ, 554, L55:
``...causes hot, X-ray emitting gas to be distributed throughout the
dense stellar wind of zeta Pup and other OB stars. Wind-shock models developed by Lucy & White (1980),
Feldmeier et al. (1997a), and others consistently failed to predict
the high levels of X-ray emission observed in the
brightest O stars like zeta Pup, leading to the suggestion that
perturbations somehow form and propagate up from the photosphere into
the wind and drive stronger shocks (Feldmeier 1995; Feldmeier, Puls, &
Pauldrach 1997b). Broadband X-ray observations of zeta Pup (Corcoran
et al. 1993; Hillier et al. 1993) indicate that some wind attenuation
is affecting the soft X-ray flux. However, with the...''
 |
Wind shell frag- mentation
|
 |
global picture
(Feldmeier et al.
2003, A&A)
|
X-RAY EMISSION LINE PROFILES
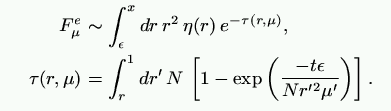
top: opt thin wind - bottom: opt thick wind
full: fragmented - dotted: homogeneous
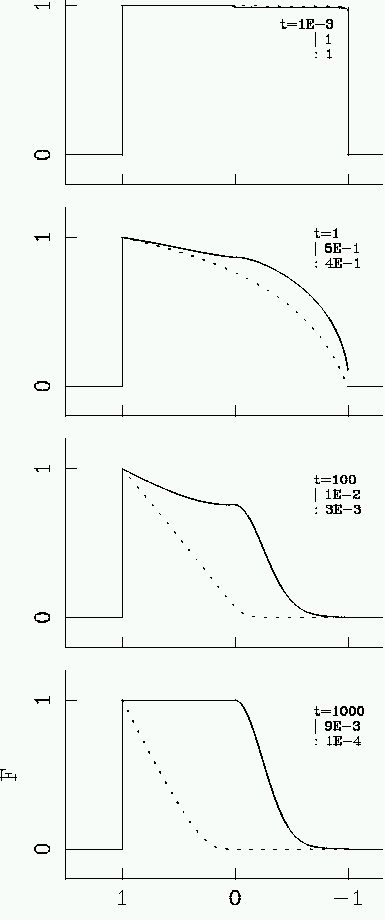
(from Feldmeier et al. 2003, A&A)
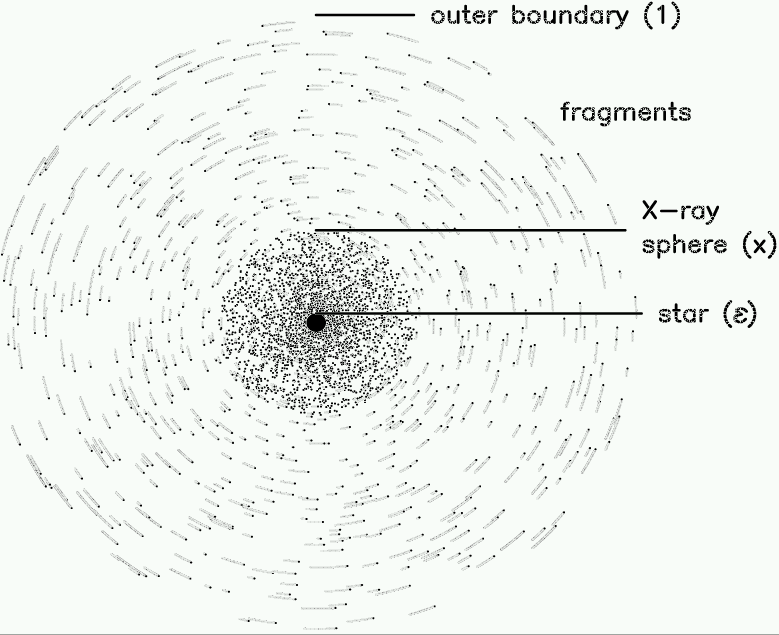
Front view of radially randomized fragments:

Sky projection of radially randomized
fragments. The front hemisphere of a unit sphere is cut into 16 384
roughly equal spherical triangles, which are subsequently randomly
redistributed between r = 0.8 and 1.0 while their angular position is
kept.
(from Oskinova et al. 2004, A&A)
Hidden opacity
(Oskinova et al. 2007, A&:A):

Reason:
opacity is hidden in highly compressed clumps
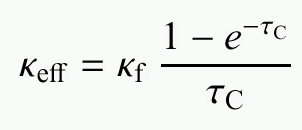
Note:
density-squared diagnostics overestimates mass-loss
(back to start)
|
Chandrasekhar
|
1943
|
Dynamical friction: momentum exchange due to gravitational force
|
 |
|
Castor, Abbott, & Klein
|
1976
|
Coulomb interactions between rad-driven ions and protons
cease in thin winds
|
|
Springmann & Pauldrach
|
1992
|
Ion runaway after decoupling (see plasma literature of 1950ies)
|
 |
|
Krticka & Kubat
|
2000
|
Ions and protons switch together (one fluid!) to slow solution branch
|
 |
|
Owocki & Puls
|
2002
|
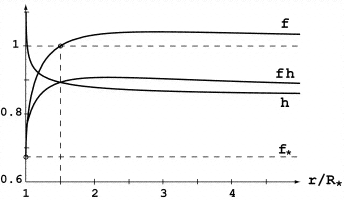
Technically, this is a shallow, subabbottic solution. Stability?
|
 |
|
Votruba, Feldmeier, & Kubat
|
2007
|
Time-dependent hydrodynamic simulations of 2-component plasma
|
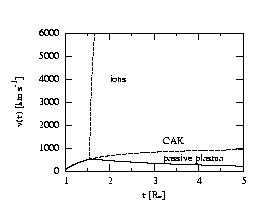 |
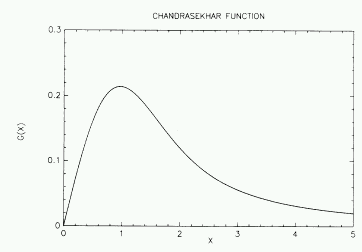
Work done: approximate
Chandrasekhar function
in order that analytic = semi-implicit solution is
possible
friction is 2nd derivative; leads to prohibitively
short Courant time step
(back to start)
From now on till end: simple SOBolev line force
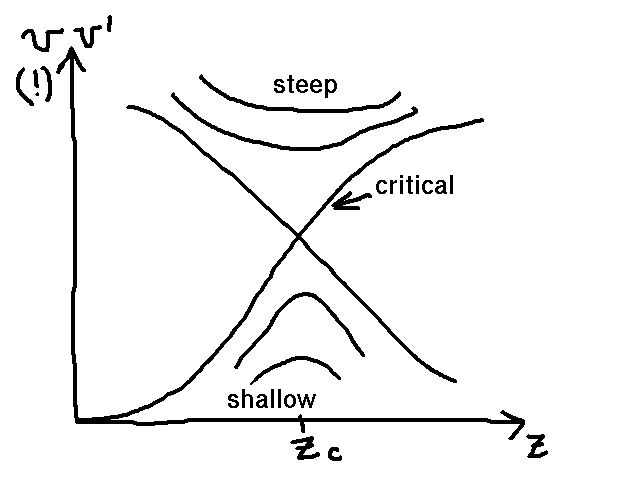
Why does wind adopt unique, critical solution out of an
infinite number of shallow and steep solutions?
| Answer: Castor et al. 1975 ApJ |
- Shallow solutions do not reach infinity
because of backpressure
- Steep solutions do not reach photosphere
because they start supersonically
- Hence, the true wind starts
shallow,
and switches at a critical point
smoothly to a steep
solution
| Further evidence: Abbott 1980 ApJ |
The CAK critical point is
to line-driven (Abbott) waves
what the sonic point is to sound waves:
an
information barrier.
- Simulations out to 10 stellar radii
converge to the
CAK solution.
But shallow solutions should be fine
out to
300 stellar radii.
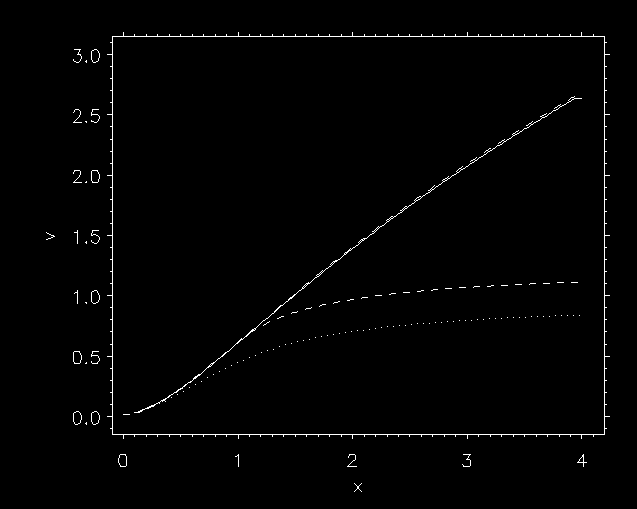 (Plase klick on the
image to see a movie)
(Plase klick on the
image to see a movie)
Artificial
convergence to the CAK solution
when pure outflow boundary
conditions are used,
and Abbott waves are NOT included in the
Courant time step.
SOB
- For disk winds, the critical solution
fails to reach
infinity, as do shallow
solutions (Feldmeier & Shlosman 1999
ApJ).
towards critical solution (Feldmeier & Shlosman 2000)
Strange dispersion of Abbott waves:
- Positive velocity slopes propagate inwards
- Negative slopes propagate outwards
Resulting in systematic acceleration of the wind: runaway
|
|
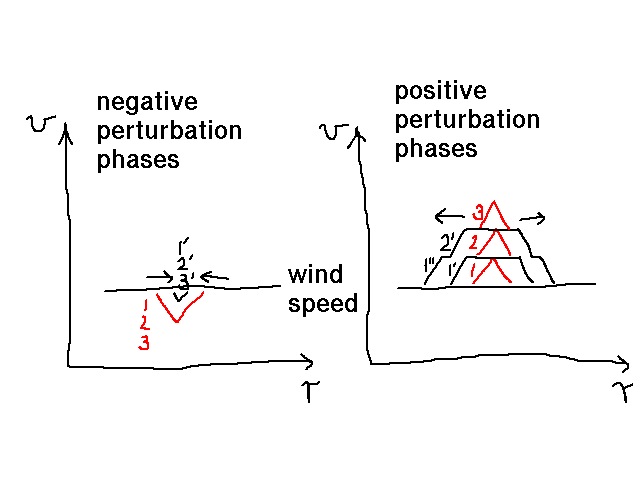
Runaway due to strange Abbott wave
dispersion: schematic
SOB
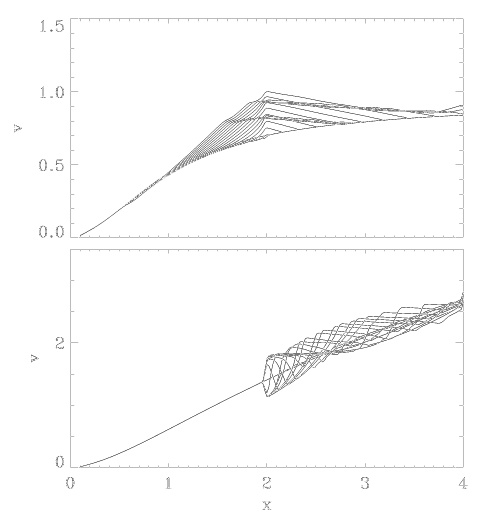
Runaway in a numerical simulation. A periodic,
sawtooth-like perturbation is maintained at x=2
The critical wind, however, is stable:
A sawtooth
perturbation at x=2 with amplitude 5% creates inward propagating
Abbott waves, but causes no runaway.
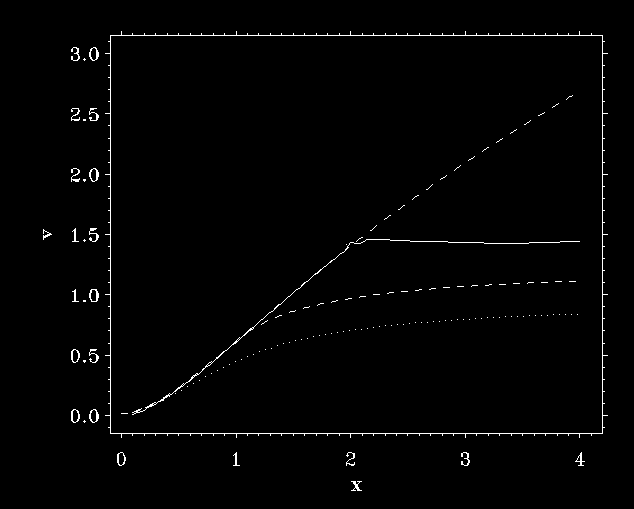
The same
perturbation but with amplitude 15% causes runaway. (The horizontal
velocity law beyond x=2 is an artifact of the applied boundary
conditions.)
SOB
| Runaway terminates when critical point forms
|
| and shuts off Abbott wave propagation
towards the photosphere. |
| If perturbations occur below the critical point
|
| runaway proceeds to overloaded solutions
|
| with supercritical mass loss rate
|
| until a generalized critical point forms.
|
| Overloaded solutions can become stationary.
|
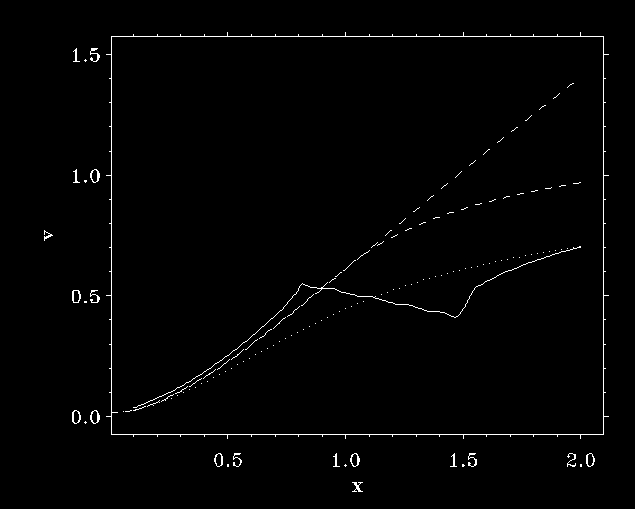
A perturbation at
x=0.8, below the critical point at x=1. The runaway proceeds to an
overloaded solution. In the broad region with negative velocity
gradient, gravity overcomes the line force. The period of the
perturbation is here ten times shorter than above.
SOB
(back to start)
Rybicki & Hummer (1978) considered v=1/r with resonance
surface (multiple radiative coupling!)
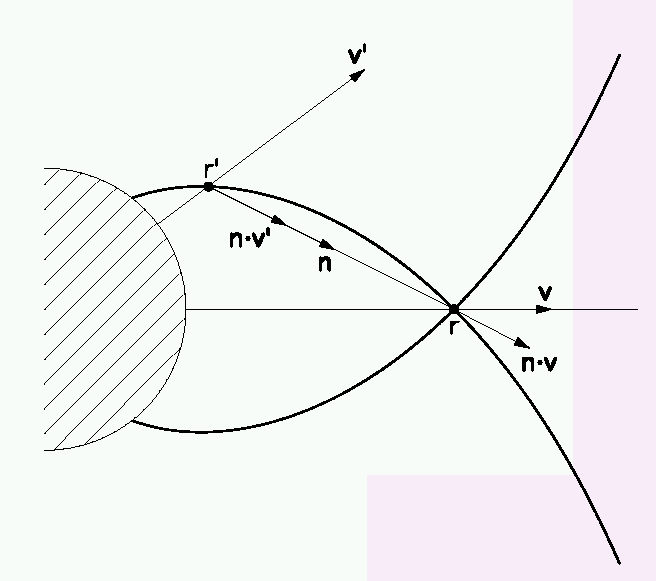
For a linear-hyperbolic-linear velocity law (e.g. due to
overloading) the shape of the resonance surface is
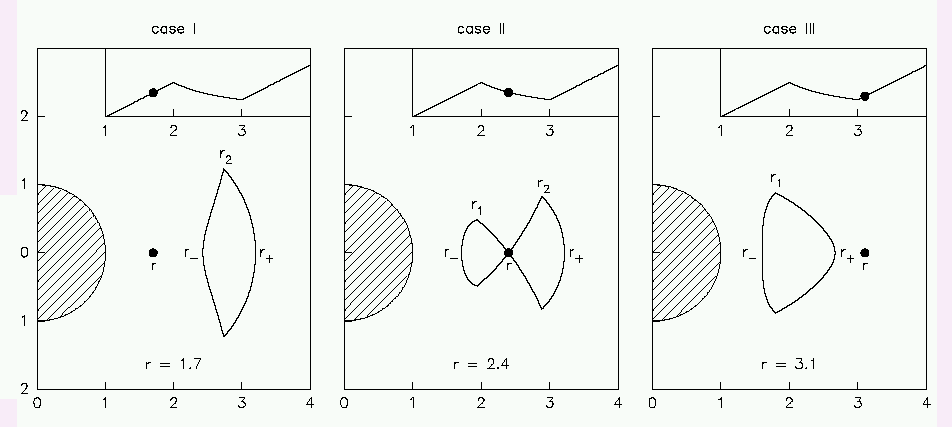
...and in the neighborhood of the outer kink.

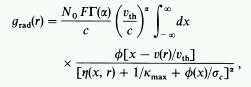 |
Pure absorption force
Owocki, Castor, & Rybicki 1988 ApJ |
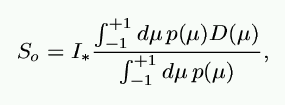 |
Smooth Source
Function: Sobolev Owocki 1991 |
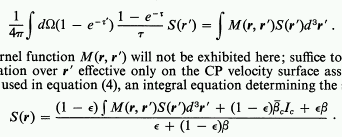 |
Iterated source
function Rybicki & Hummer 1978
ApJ |
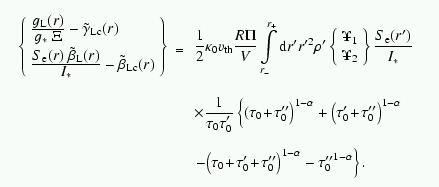
|
Iterated SF for
3-point coupling Feldmeier & Nikutta
2006 A&A |
|
Alternative method
Baron & Hauschildt 2004 |
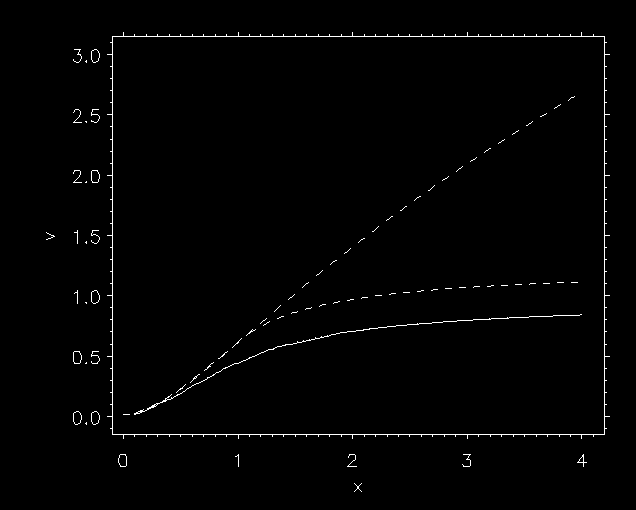
The wind structure after S-iteration (thick line) vs CAK wind (thin
line) is
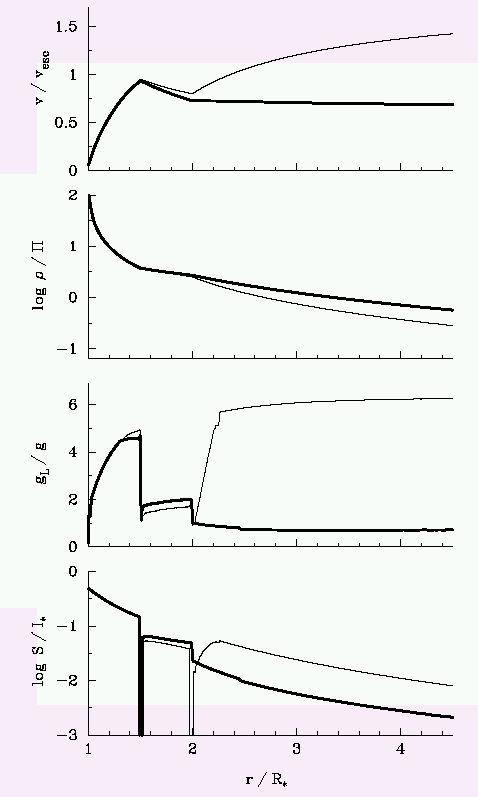
(back to start)
Ongoing work with Dennis Raetzel
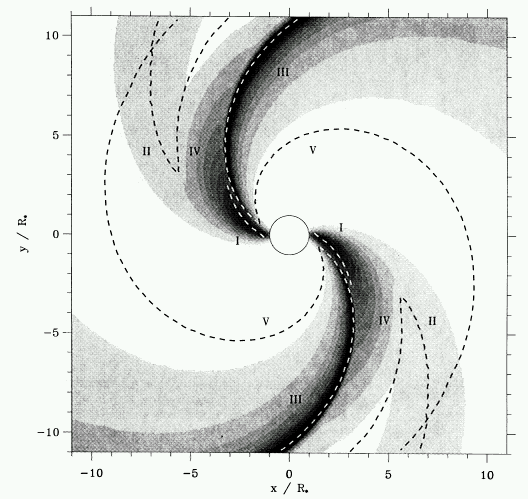
Cranmer & Owocki 1996 ApJ
(back to start)
still: SOB
Winds from accretion disks in
- Protostars
- Cataclysmic variables
- Quasars
Simplifying
assumption so far:
protostellar winds are magnetically
driven...
|
... winds from cataclysmic variables are line driven.
|
Here: combination of magnetic and radiative driving
|
| Two basic differences between star and disk wind
launching |
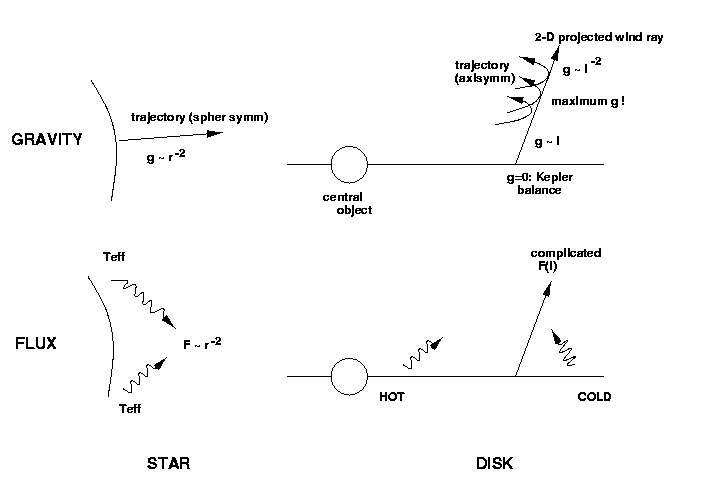
Gravity and radiation flux have independent maxima as function of
height: up to 3 critical
points. (For stars: 1)
| Short history of papers on line driven disk
winds |
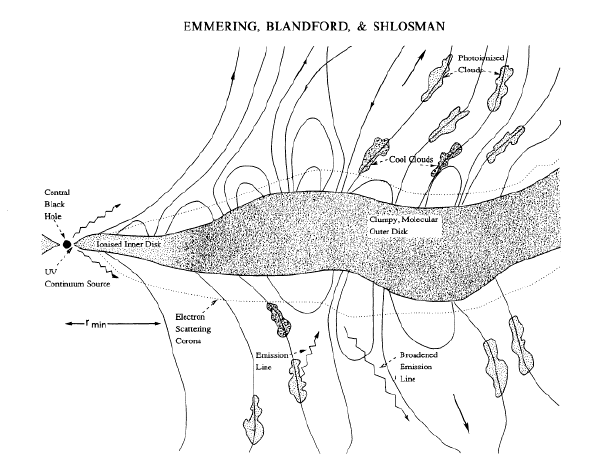
| Shlosman 1985. Quasar winds with
local launching due to disk radiative flux. Bright central region
is shielded by absorption in disk atmosphere.
|
| Shlosman & Vitello 1988.
There is no critical point for vertical launching ... (and many
more approximations) -> Ionization gradients central?
|
| de Kool & Begelmann 1994.
Similarity solution for magnetic wind with scaled-up continuum
radiation driving (no true line driving).
|
| Feldmeier & Shlosman 1999. Analytical solution along straight wind cones. 2-D
eigenvalue problem: mass loss rate and wind tilt
angle. |
| Proga, Stone & Drew 1998. First
time-dependent wind models using Zeus 2-D code.
|
(another) disk wind movie
| Results for line driven disk winds at
B=0 |
- mass loss rates in good agreement with CAK theory
- however: much smaller than single scattering limit :
thin winds
- inherent wind variability: streamers. Origin unclear
| Recent MHD + rad hydro simulations |
Central questions:
- can magnetic field increase mass loss?: B=0 winds are presently
far too thin
- can radiative launching overcome problems with pure
magneto-thermal launching? (Ogilvie & Livio 1998)
| Classical scenario for MHD winds |
magnetic pressure >> gas pressure ("corona")
-->
corotating, rigid poloidal magnetic field lines
-->
for tilts > 30 deg, gas flows away freely from the disk:
(gas) beads on a (magnetic) wire
|
we find that Zeus 2-D favors another flow scenario |
first suggested theoretically by Contopoulos 1995. |
|
| Here, only a
toroidal magnetic fields occurs.
|
| Wind is launched via
Lorentz force
due to vertical gradients of the toroidal field.
|
By contrast,
Blandford & Payne wind is launched via
centrifugal force due to stiff poloidal
field lines.
|
|

The Lorentz force j x B ~ (rot B) x B points upwards.
| A dynamical mixture of Blandford-Payne and
Contopoulos winds? |
|
Our models show an interplay
between poloidal and toroidal fields:
|
only for sufficiently strong poloidal fields,
a Kelvin-Helmholtz vortex sheet forms
|
at the edge of the star with the disk, and extending outwards
at a polar angle of 45 deg.
|
|
The K-H eddies carry the toroidal field above the CAK critical
point
|
which corresponds to the bottleneck of the flow.
|
The Lorentz force from the toroidal field can then assist in
carrying enhanced mass loss.
|
By contrast, models with pure toroidal fiels (pure Contopoulos
model) show smaller, CAK mass loss rates.
|

|
Kelvin-
Helmholtz
wave
in poloidal
magnetic
field
unit arrow
(top right) =
0.5 Gauss
please click on the image to see
the movie
|








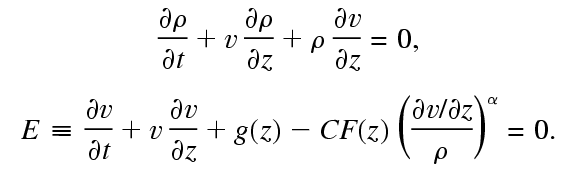

 (Please klick on the image)
(Please klick on the image)









 Favored scenario:
Favored scenario: Strong oscillatory thermal instability
Strong oscillatory thermal instability 



















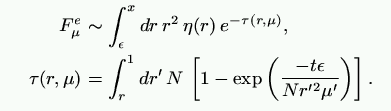



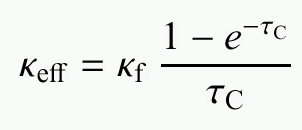







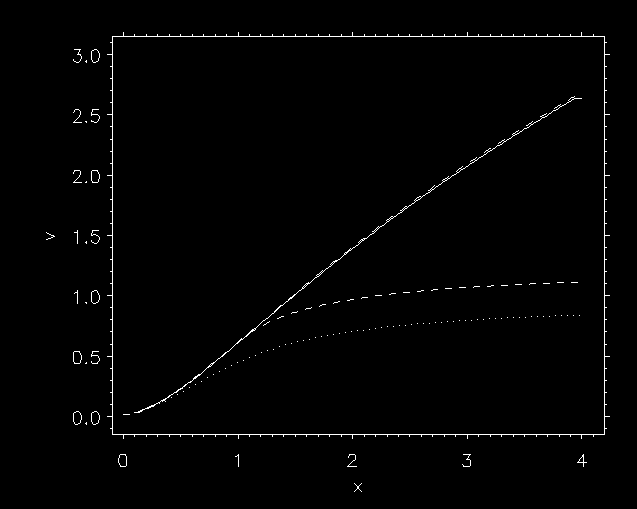 (Plase klick on the
image to see a movie)
(Plase klick on the
image to see a movie) 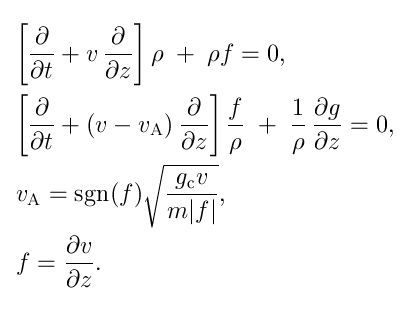








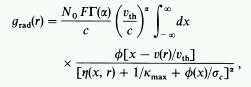
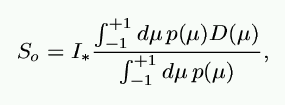
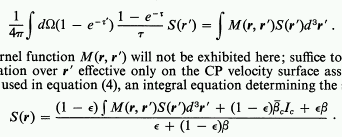
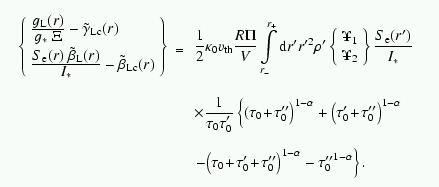
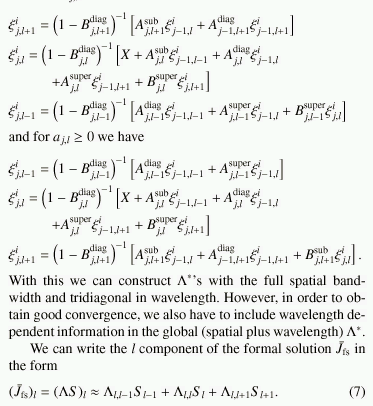






 NASA press release, April 26, 2001
NASA press release, April 26, 2001